2020 AMC 12A Problems/Problem 12
Contents
Problem
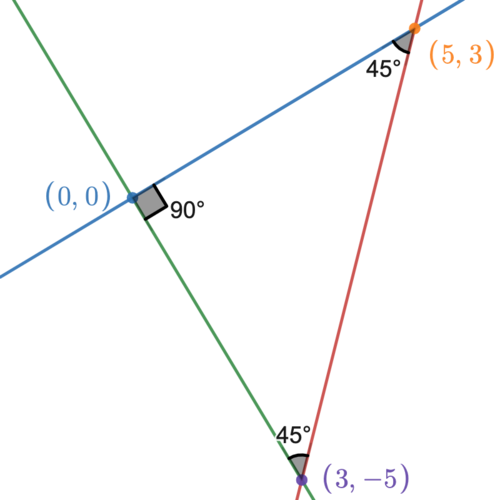
Line ![]() in the coordinate plane has equation
in the coordinate plane has equation ![]() . This line is rotated
. This line is rotated ![]() counterclockwise about the point
counterclockwise about the point ![]() to obtain line
to obtain line ![]() . What is the
. What is the ![]() -coordinate of the
-coordinate of the ![]() -intercept of line
-intercept of line ![]()
![]()
Solution 1
The slope of the line is ![]() . We must transform it by
. We must transform it by ![]() .
.
![]() creates an isosceles right triangle, since the sum of the angles of the triangle must be
creates an isosceles right triangle, since the sum of the angles of the triangle must be ![]() and one angle is
and one angle is ![]() . This means the last leg angle must also be
. This means the last leg angle must also be ![]() .
.
In the isosceles right triangle, the two legs are congruent. We can therefore construct an isosceles right triangle with a line of ![]() slope on graph paper. That line with
slope on graph paper. That line with ![]() slope starts at
slope starts at ![]() and will go to
and will go to ![]() , the vector
, the vector ![]() .
.
Construct another line from ![]() to
to ![]() , the vector
, the vector ![]() . This is
. This is ![]() and equal to the original line segment. The difference between the two vectors is
and equal to the original line segment. The difference between the two vectors is ![]() , which is the slope
, which is the slope ![]() , and that is the slope of line
, and that is the slope of line ![]() .
.
Furthermore, the equation ![]() passes straight through
passes straight through ![]() since
since ![]() , which means that any rotations about
, which means that any rotations about ![]() would contain
would contain ![]() . We can create a line of slope
. We can create a line of slope ![]() through
through ![]() . The
. The ![]() -intercept is therefore
-intercept is therefore ![]() ~lopkiloinm ~ShawnX (diagram)
~lopkiloinm ~ShawnX (diagram)
Solution 2
Since the slope of the line is ![]() , and the angle we are rotating around is x, then
, and the angle we are rotating around is x, then ![]()
![]()
Hence, the slope of the rotated line is ![]() . Since we know the line intersects the point
. Since we know the line intersects the point ![]() , then we know the line is
, then we know the line is ![]() . Set
. Set ![]() to find the x-intercept, and so
to find the x-intercept, and so ![]()
~Solution by IronicNinja
Solution 3
![[asy] draw((0,0)--(20, 0)--(20, 20)--(0, 20)--cycle); draw((20, 20)--(0, 8)); draw((15, 0)--(20, 20)); dot("$P$", (20, 20)); dot("$A$", (0, 8), dir(75)); dot("$B$", (15, 0), dir(45)); dot("$X$", (20, 0)); dot("$Y$", (0, 20), dir(50)); [/asy]](http://latex.artofproblemsolving.com/d/7/c/d7ce7cf28bf03e187cb3bf0b06f3c438043067f4.png)
Let ![]() be
be ![]() and
and ![]() be
be ![]() and
and ![]() respectively. Since the slope of the line is
respectively. Since the slope of the line is ![]() we know that
we know that ![]() Segments
Segments ![]() and
and ![]() represent the before and after of rotating
represent the before and after of rotating ![]() by 45 counterclockwise. Thus,
by 45 counterclockwise. Thus, ![]() and
and ![]() by tangent addition formula. Since
by tangent addition formula. Since ![]() is 5 and the sidelength of the square is 20 the answer is
is 5 and the sidelength of the square is 20 the answer is ![]()
Solution 4 (Cheap)
Using the protractor you brought, carefully graph the equation and rotate the given line ![]() counter-clockwise about the point
counter-clockwise about the point ![]() . Scaling everything down by a factor of 5 makes this process easier.
. Scaling everything down by a factor of 5 makes this process easier.
It should then become fairly obvious that the x intercept is ![]() (only use this as a last resort).
(only use this as a last resort).
~Silverdragon
Solution 5 (Rotation Matrix)
First note that the given line goes through ![]() with a slope of
with a slope of ![]() . This means that
. This means that ![]() is on the line. Now consider translating the graph so that
is on the line. Now consider translating the graph so that ![]() goes to the origin, then
goes to the origin, then ![]() becomes
becomes ![]() . We now rotate the line
. We now rotate the line ![]() about the origin using a rotation matrix. This maps
about the origin using a rotation matrix. This maps ![]() to
to
![\[\begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}\begin{bmatrix} 5 \\ 3\end{bmatrix}=\begin{bmatrix}\sqrt{2} \\ 4\sqrt{2}\end{bmatrix}\]](http://latex.artofproblemsolving.com/9/9/c/99cf664db97e49fd09061d50fe45a2d45c176ced.png) The line through the origin and
The line through the origin and ![]() has slope
has slope ![]() . Translating this line so that the origin is mapped to
. Translating this line so that the origin is mapped to ![]() , we find that the equation for the new line is
, we find that the equation for the new line is ![]() , meaning that the
, meaning that the ![]() -intercept is
-intercept is ![]() .
.
Solution 6 (Angle Bisector)
Note ![]() is on the line. Construct the perpendicular line
is on the line. Construct the perpendicular line ![]() . This creates a right triangle that intersects the x-axis at
. This creates a right triangle that intersects the x-axis at ![]() and
and ![]() a distance of
a distance of ![]() apart. The
apart. The ![]() transformation will bisect the right angle.
The angle bisector theorem tells us the
transformation will bisect the right angle.
The angle bisector theorem tells us the ![]() will split in ratio to the lengths of the sides.
These are
will split in ratio to the lengths of the sides.
These are ![]() and
and  and
and ![]() . Thus the x intercept will split the line from
. Thus the x intercept will split the line from ![]() to
to ![]() into a ratio of
into a ratio of ![]() making the x-intercept
making the x-intercept ![]() .
.
Solution 7 (Complex Numbers)
Converting to the complex plane, we can see that two numbers on the line are ![]() and
and ![]() . Translating
. Translating ![]() to the origin, we get
to the origin, we get ![]() and
and ![]() . Multiplying each of them by
. Multiplying each of them by ![]() , we get
, we get ![]() and
and ![]() . This line has a slope of
. This line has a slope of ![]() . Now, back to the cartesian plane. We have a line passing through
. Now, back to the cartesian plane. We have a line passing through ![]() with slope
with slope ![]() which gives the equation as
which gives the equation as ![]() which implies the
which implies the ![]() coordinate of the
coordinate of the ![]() intercept is
intercept is ![]() .
.
~rocketsri (minor error corrected by kn07)
Solution 8 (quick)
A quick check tells us that ![]() falls on the given line. Common sense tells us that if the slope of the original line is
falls on the given line. Common sense tells us that if the slope of the original line is ![]() , or 45 degrees from the horizontal, a 45 counter clockwise rotation will result in a vertical line, and the x-intercept will be
, or 45 degrees from the horizontal, a 45 counter clockwise rotation will result in a vertical line, and the x-intercept will be ![]() .
Thinking of a 45 degree counter clockwise rotation as a 90 degree counter clockwise rotation that is bisected will helps in visualizing this line of reasoning.
Therefore, it follows that if the original line is made steeper, then the x-intercept will move away from
.
Thinking of a 45 degree counter clockwise rotation as a 90 degree counter clockwise rotation that is bisected will helps in visualizing this line of reasoning.
Therefore, it follows that if the original line is made steeper, then the x-intercept will move away from ![]() to the right. If the original line is made lower, then the opposite will happen. Our given line has slope
to the right. If the original line is made lower, then the opposite will happen. Our given line has slope ![]() , so the answer must be
, so the answer must be ![]() or
or ![]() .
. ![]() can be eliminated because an x-intercept of
can be eliminated because an x-intercept of ![]() can only occur when the original line is horizontal. In conclusion, the answer must be
can only occur when the original line is horizontal. In conclusion, the answer must be ![]() .
.
~jackshi2006
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 11 |
Followed by Problem 13 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.