2018 AIME II Problems/Problem 14
Contents
Problem
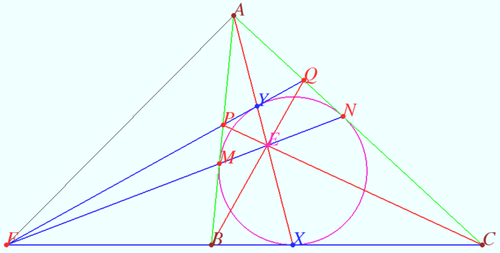
The incircle ![]() of triangle
of triangle ![]() is tangent to
is tangent to ![]() at
at ![]() . Let
. Let ![]() be the other intersection of
be the other intersection of ![]() with
with ![]() . Points
. Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() , respectively, so that
, respectively, so that ![]() is tangent to
is tangent to ![]() at
at ![]() . Assume that
. Assume that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
![[asy] size(200); import olympiad; defaultpen(linewidth(1)+fontsize(12)); pair A,B,C,P,Q,Wp,X,Y,Z; B=origin; C=(6.75,0); A=IP(CR(B,7),CR(C,8)); path c=incircle(A,B,C); Wp=IP(c,A--C); Z=IP(c,A--B); X=IP(c,B--C); Y=IP(c,A--X); pair I=incenter(A,B,C); P=extension(A,B,Y,Y+dir(90)*(Y-I)); Q=extension(A,C,P,Y); draw(A--B--C--cycle, black+1); draw(c^^A--X^^P--Q); pen p=4+black; dot("$A$",A,N,p); dot("$B$",B,SW,p); dot("$C$",C,SE,p); dot("$X$",X,S,p); dot("$Y$",Y,dir(55),p); dot("$W$",Wp,E,p); dot("$Z$",Z,W,p); dot("$P$",P,W,p); dot("$Q$",Q,E,p); MA("\beta",C,X,A,0.3,black); MA("\alpha",B,A,X,0.7,black); [/asy]](http://latex.artofproblemsolving.com/4/0/7/4073dcacb93163e2fca4cd2a02d09ff864a1f50b.png)
Solution 1
Let the sides ![]() and
and ![]() be tangent to
be tangent to ![]() at
at ![]() and
and ![]() , respectively. Let
, respectively. Let ![]() and
and ![]() . Because
. Because ![]() and
and ![]() are both tangent to
are both tangent to ![]() and
and ![]() and
and ![]() subtend the same arc of
subtend the same arc of ![]() , it follows that
, it follows that ![]() . By equal tangents,
. By equal tangents, ![]() . Applying the Law of Sines to
. Applying the Law of Sines to ![]() yields
yields ![]() Similarly, applying the Law of Sines to
Similarly, applying the Law of Sines to ![]() gives
gives ![]() It follows that
It follows that ![]() implying
implying ![]() . Applying the same argument to
. Applying the same argument to ![]() yields
yields ![]() from which
from which ![]() . The requested sum is
. The requested sum is ![]() .
.
Solution 2 (Projective)
Let the incircle of ![]() be tangent to
be tangent to ![]() and
and ![]() at
at ![]() and
and ![]() . By Brianchon's theorem on tangential hexagons
. By Brianchon's theorem on tangential hexagons ![]() and
and ![]() , we know that
, we know that ![]() and
and ![]() are concurrent at a point
are concurrent at a point ![]() . Let
. Let ![]() . Then by La Hire's
. Then by La Hire's ![]() lies on the polar of
lies on the polar of ![]() so
so ![]() lies on the polar of
lies on the polar of ![]() . Therefore,
. Therefore, ![]() also passes through
also passes through ![]() . Then projecting through
. Then projecting through ![]() , we have
, we have
![]() Therefore,
Therefore, ![]() . Since
. Since ![]() we know that
we know that ![]() and
and ![]() . Therefore,
. Therefore, ![]() and
and ![]() . Since
. Since ![]() , we also have
, we also have ![]() . Solving for
. Solving for ![]() , we obtain
, we obtain ![]() .
😃
-Vfire
.
😃
-Vfire
Solution 3 (Combination of Law of Sine and Law of Cosine)
Let the center of the incircle of ![]() be
be ![]() . Link
. Link ![]() and
and ![]() . Then we have
. Then we have ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let the incircle of ![]() be tangent to
be tangent to ![]() and
and ![]() at
at ![]() and
and ![]() , let
, let ![]() and
and ![]() .
.
Use Law of Sine in ![]() and
and ![]() , we have
, we have
![]()
![]()
therefore we have
![]()
Solve this equation, we have ![]()
As a result, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
So, ![]()
Use Law of Cosine in ![]() and
and ![]() , we have
, we have
![]()

And we have
![]()
So

Solve this equation, we have ![]()
As a result, ![]()
So, the final answer of this question is ![]()
~Solution by ![]() (Frank FYC)
(Frank FYC)
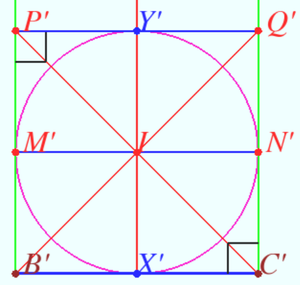
Solution 4 (Projective geometry)
Claim
Let the sides ![]() and
and ![]() be tangent to
be tangent to ![]() at
at ![]() and
and ![]() , respectively. Then
lines
, respectively. Then
lines ![]() and
and ![]() are concurrent and lines
are concurrent and lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Let ![]() be point of crossing
be point of crossing ![]() and
and ![]() We make projective transformation such that circle
We make projective transformation such that circle ![]() maps into the circle and point
maps into the circle and point ![]() maps into the center of new circle point
maps into the center of new circle point ![]() We denote images using notification
We denote images using notification ![]()
![]() maps into
maps into ![]() , so lines
, so lines ![]() and
and ![]() be the diameters.
This implies
be the diameters.
This implies ![]() be a square.
be a square.
Therefore ![]() be the diameter
be the diameter ![]() be diagonals of the square.
be diagonals of the square. ![]() and
and ![]() be midlines which crossing in the center
be midlines which crossing in the center ![]() Therefore lines
Therefore lines ![]() and
and ![]() are concurrent.
are concurrent.
Lines ![]() and
and ![]() are concurrent.
are concurrent.
Solution
The cross-ratio associated with a list of four collinear points ![]() is defined as
is defined as ![]() The cross-ratio be projective invariant of a quadruple of collinear points, so
The cross-ratio be projective invariant of a quadruple of collinear points, so
![]()
![]()
![]()
![]()
For visuals only, I will show how one can find the perceptor ![]() and the image’s plane.
and the image’s plane.
![]() is image of inversion
is image of inversion ![]() with respect
with respect ![]()
![]() is the diameter of
is the diameter of ![]() are collinear.
are collinear.
![]() is diameter of
is diameter of ![]() .
.
Plane of images is perpendicular to ![]()
Last diagram shows the result of transformation. Transformation is possible. The end.
vladimir.shelomovskii@gmail.com, vvsss
Video Solution by Mop 2024
~r00tsOfUnity
See Also
| 2018 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.