2018 AIME I Problems/Problem 15

Problem 15

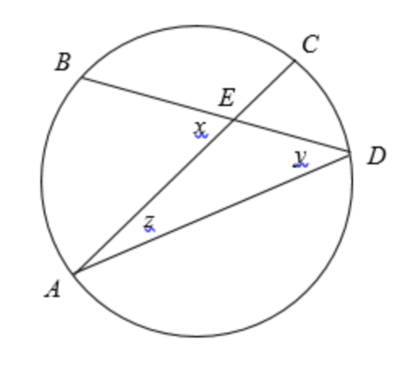
David found four sticks of different lengths that can be used to form three non-congruent convex cyclic quadrilaterals, $A,\text{ }B,\text{ }C$ , which can each be inscribed in a circle with radius $1$ . Let $\varphi_A$ denote the measure of the acute angle made by the diagonals of quadrilateral $A$ , and define $\varphi_B$ and $\varphi_C$ similarly. Suppose that $\sin\varphi_A=\tfrac{2}{3}$ , $\sin\varphi_B=\tfrac{3}{5}$ , and $\sin\varphi_C=\tfrac{6}{7}$ . All three quadrilaterals have the same area $K$ , which can be written in the form $\dfrac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

Solution 1

Suppose our four sides lengths cut out arc lengths of $2a$ , $2b$ , $2c$ , and $2d$ , where $a+b+c+d=180^\circ$ . Then, we only have to consider which arc is opposite $2a$ . These are our three cases, so $\varphi_A=a+c$ $\varphi_B=a+b$ $\varphi_C=a+d$ Our first case involves quadrilateral $ABCD$ with $\overarc{AB}=2a$ , $\overarc{BC}=2b$ , $\overarc{CD}=2c$ , and $\overarc{DA}=2d$ .

Then, by Law of Sines, $AC=2\sin\left(\frac{\overarc{ABC}}{2}\right)=2\sin(a+b)$ and $BD=2\sin\left(\frac{\overarc{BCD}}{2}\right)=2\sin(a+d)$ . Therefore,

$K=\frac{1}{2}\cdot AC\cdot BD\cdot \sin(\varphi_A)=2\sin\varphi_A\sin\varphi_B\sin\varphi_C=\frac{24}{35},$ so our answer is $24+35=\boxed{059}$ .

Note that the conditions of the problem are satisfied when the lengths of the four sticks are about $0.32, 0.91, 1.06, 1.82$ .

By S.B.

Note

The solution uses $\varphi_A=a+c.$

We can see that this follows because $\varphi_A = \frac12 (2a+2c)=a+c,$ where $a$ and $c$ are the central angles of opposite sides.

Solution 2

Suppose the four side lengths of the quadrilateral cut out arc lengths of $2a$ , $2b$ , $2c$ , and $2d$ . $a+b+c+d=180^\circ$ . Therefore, without losing generality,

$\varphi_A=a+b$ $\varphi_B=b+c$ $\varphi_C=a+c$

$(1)+(3)-(2)$ , $(1)+(2)-(3)$ , and $(2)+(3)-(1)$ yields

$2a=\varphi_A+\varphi_C-\varphi_B$ $2b=\varphi_A+\varphi_B-\varphi_C$ $2c=\varphi_B+\varphi_C-\varphi_A$

Because $2d=360^\circ-2a-2b-2c,$ Therefore,

$2d=360^\circ-\varphi_A-\varphi_B-\varphi_C$

Using the sum-to-product identities, our area of the quadrilateral $K$ then would be

$\begin{align*} K&=\frac{1}{2}(\sin(2a)+\sin(2b)+\sin(2c)+\sin(2d))\\ &=\frac{1}{2}(\sin(\varphi_A+\varphi_B-\varphi_C)+\sin(\varphi_B+\varphi_C-\varphi_A)+\sin(\varphi_C+\varphi_A-\varphi_B)-\sin(\varphi_A+\varphi_B+\varphi_C))\\ &=\frac{1}{2}(2\sin\varphi_B\cos(\varphi_A-\varphi_C)-2\sin\varphi_B\cos(\varphi_A+\varphi_C))\\ &=\frac{1}{2}\cdot2\cdot2\sin\varphi_A\sin\varphi_B\sin\varphi_C\\ &=2\sin\varphi_A\sin\varphi_B\sin\varphi_C\\ &=\frac{24}{35}\\ \end{align*}$

Therefore, our answer is $24+35=\boxed{059}$ .

~Solution by eric-z

Solution 3

Let the four stick lengths be $a$ , $b$ , $c$ , and $d$ . WLOG, let’s say that quadrilateral $A$ has sides $a$ and $d$ opposite each other, quadrilateral $B$ has sides $b$ and $d$ opposite each other, and quadrilateral $C$ has sides $c$ and $d$ opposite each other. The area of a convex quadrilateral can be written as $\frac{1}{2} d_1 d_2 \sin{\theta}$ , where $d_1$ and $d_2$ are the lengths of the diagonals of the quadrilateral and $\theta$ is the angle formed by the intersection of $d_1$ and $d_2$ . By Ptolemy's theorem $d_1 d_2 = ad+bc$ for quadrilateral $A$ , so, defining $K_A$ as the area of $A$ , $K_A = \frac{1}{2} (ad+bc)\sin{\varphi_A}$ Similarly, for quadrilaterals $B$ and $C$ , $K_B = \frac{1}{2} (bd+ac)\sin{\varphi_B}$ and $K_C = \frac{1}{2} (cd+ab)\sin{\varphi_C}$ Multiplying the three equations and rearranging, we see that $K_A K_B K_C = \frac{1}{8} (ab+cd)(ac+bd)(ad+bc)\sin{\varphi_A}\sin{\varphi_B}\sin{\varphi_B}$ $K^3 = \frac{1}{8} (ab+cd)(ac+bd)(ad+bc)\left(\frac{2}{3}\right) \left(\frac{3}{5}\right) \left(\frac{6}{7}\right)$ $\frac{70}{3}K^3 = (ab+cd)(ac+bd)(ad+bc)$ The circumradius $R$ of a cyclic quadrilateral with side lengths $a$ , $b$ , $c$ , and $d$ and area $K$ can be computed as $R = \frac{\sqrt{(ab+cd)(ac+bd)(ad+bc)}}{4K}$ . Inserting what we know, $1 = \frac{\sqrt{\frac{70}{3}K^3}}{4K}\quad \Rightarrow \quad 16K^2 = \frac{70}{3}K^3\quad \Rightarrow \quad \frac{24}{35} = K$ So our answer is $24 + 35 = \boxed{059}$ .

~Solution by divij04

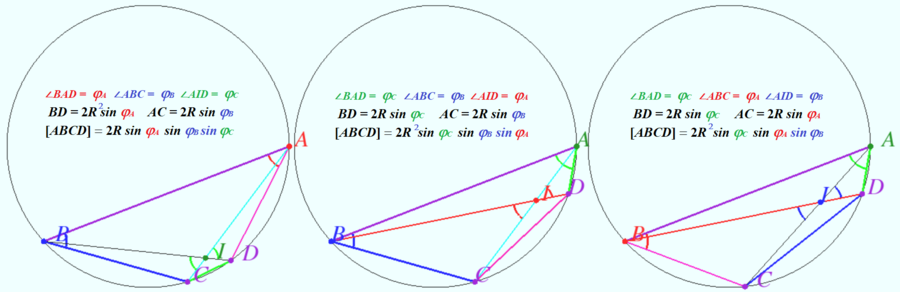
Solution 4 (No words)

vladimir.shelomovskii@gmail.com, vvsss

Solution 5

Let the sides of the quadrilaterals be $a,b,c,$ and $d$ in some order such that $A$ has $a$ opposite of $c$ , $B$ has $a$ opposite of $b$ , and $C$ has $a$ opposite of $d$ . Then, let the diagonals of $A$ be $e$ and $f$ . Similarly to solution $2$ , we get that $\tfrac{2}{3}(ac+bd)=\tfrac{3}{5}(ab+cd)=\tfrac{6}{7}(ad+bc)=2K$ , but this is also equal to $2\cdot\tfrac{eab+ecd}{4(1)}=2\cdot\tfrac{fad+fbc}{4(1)}$ using the area formula for a triangle using the circumradius and the sides, so $\tfrac{e(ab+cd)}{2}=\tfrac{3}{5}(ab+cd)$ and $\tfrac{f(ad+bc)}{2}=\tfrac{6}{7}(ad+bc)$ . Solving for $e$ and $f$ , we get that $e=\tfrac{6}{5}$ and $f=\tfrac{12}{7}$ , but $K=\tfrac{1}{2}\cdot\tfrac{2}{3}\cdot{}ef$ , similarly to solution $2$ , so $K=\tfrac{24}{35}$ and the answer is $24+35=\boxed{059}$ .

Video Solution by MOP 2024

https://youtu.be/oPG4MHzpvcc

~r00tsOfUnity

2018 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search