2005 AIME II Problems/Problem 15
Contents
Problem
Let ![]() and
and ![]() denote the circles
denote the circles ![]() and
and ![]() respectively. Let
respectively. Let ![]() be the smallest positive value of
be the smallest positive value of ![]() for which the line
for which the line ![]() contains the center of a circle that is externally tangent to
contains the center of a circle that is externally tangent to ![]() and internally tangent to
and internally tangent to ![]() Given that
Given that ![]() where
where ![]() and
and ![]() are relatively prime integers, find
are relatively prime integers, find ![]()
Solution 1
Rewrite the given equations as ![]() and
and ![]() .
.
Let ![]() have center
have center ![]() and radius
and radius ![]() . Now, if two circles with radii
. Now, if two circles with radii ![]() and
and ![]() are externally tangent, then the distance between their centers is
are externally tangent, then the distance between their centers is ![]() , and if they are internally tangent, it is
, and if they are internally tangent, it is ![]() . So we have
. So we have

Solving for ![]() in both equations and setting them equal, then simplifying, yields
in both equations and setting them equal, then simplifying, yields

Squaring again and canceling yields ![]()
So the locus of points that can be the center of the circle with the desired properties is an ellipse.
![[asy] size(220); pointpen = black; pen d = linewidth(0.7); pathpen = d; pair A = (-5, 12), B = (5, 12), C = (0, 0); D(CR(A,16));D(CR(B,4));D(shift((0,12)) * yscale(3^.5 / 2) * CR(C,10), linetype("2 2") + d + red); D((0,30)--(0,-10),Arrows(4));D((15,0)--(-25,0),Arrows(4));D((0,0)--MP("y=ax",(14,14 * (69/100)^.5),E),EndArrow(4)); void bluecirc (real x) { pair P = (x, (3 * (25 - x^2 / 4))^.5 + 12); dot(P, blue); D(CR(P, ((P.x - 5)^2 + (P.y - 12)^2)^.5 - 4) , blue + d + linetype("4 4")); } bluecirc(-9.2); bluecirc(-4); bluecirc(3); [/asy]](http://latex.artofproblemsolving.com/3/9/5/3952f7611dcec95c9d68289eb69eb74de86b62bc.png)
Since the center lies on the line ![]() , we substitute for
, we substitute for ![]() and expand:
and expand:
![]()
We want the value of ![]() that makes the line
that makes the line ![]() tangent to the ellipse, which will mean that for that choice of
tangent to the ellipse, which will mean that for that choice of ![]() there is only one solution to the most recent equation. But a quadratic has one solution iff its discriminant is
there is only one solution to the most recent equation. But a quadratic has one solution iff its discriminant is ![]() , so
, so ![]() .
.
Solving yields ![]() , so the answer is
, so the answer is ![]() .
.
Solution 2
As above, we rewrite the equations as ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . If a circle with center
. If a circle with center ![]() and radius
and radius ![]() is externally tangent to
is externally tangent to ![]() and internally tangent to
and internally tangent to ![]() , then
, then ![]() and
and ![]() . Therefore,
. Therefore, ![]() . In particular, the locus of points
. In particular, the locus of points ![]() that can be centers of circles must be an ellipse with foci
that can be centers of circles must be an ellipse with foci ![]() and
and ![]() and major axis
and major axis ![]() .
.
Clearly, the minimum value of the slope ![]() will occur when the line
will occur when the line ![]() is tangent to this ellipse. Suppose that this point of tangency is denoted by
is tangent to this ellipse. Suppose that this point of tangency is denoted by ![]() , and the line
, and the line ![]() is denoted by
is denoted by ![]() . Then we reflect the ellipse over
. Then we reflect the ellipse over ![]() to a new ellipse with foci
to a new ellipse with foci ![]() and
and ![]() as shown below.
as shown below.
![[asy] size(220); pair F1 = (-5, 12), F2 = (5, 12),C=(0,12); draw(circle(F1,16)); draw(circle(F2,4)); draw(ellipse(C,10,5*sqrt(3))); xaxis("$x$",Arrows); yaxis("$y$",Arrows); dot(F1^^F2^^C); real l(real x) {return sqrt(69)*x/10;} path g=graph(l,-7,14); draw(g); draw(reflect((0,0),(10,l(10)))*ellipse(C,10,5*sqrt(3))); pair T=intersectionpoint(ellipse(C,10,5*sqrt(3)),(0,0)--(10,l(10))); dot(T); pair F1P=reflect((0,0),(10,l(10)))*F1; pair F2P=reflect((0,0),(10,l(10)))*F2; dot(F1P^^F2P); dot((0,0)); label("$F_1$",F1,N,fontsize(9)); label("$F_2$",F2,N,fontsize(9)); label("$F_1'$",F1P,SE,fontsize(9)); label("$F_2'$",F2P,SE,fontsize(9)); label("$O$",(0,0),NW,fontsize(9)); label("$\ell$",(13,l(13)),SE,fontsize(9)); label("$T$",T,NW,fontsize(9)); draw((0,0)--F1--F2--F2P--F1P--cycle); draw(F1--F2P^^F2--F1P); [/asy]](http://latex.artofproblemsolving.com/3/9/f/39f7436c9b561798a9afaf9bddc9c97fd6de020d.png)
By the reflection property of ellipses (i.e., the angle of incidence to a tangent line is equal to the angle of reflection for any path that travels between the foci), we know that ![]() ,
, ![]() , and
, and ![]() are collinear, and similarly,
are collinear, and similarly, ![]() ,
, ![]() and
and ![]() are collinear. Therefore,
are collinear. Therefore, ![]() is a pentagon with
is a pentagon with ![]() ,
, ![]() , and
, and ![]() . Note that
. Note that ![]() bisects
bisects ![]() . We can bisect this angle by bisecting
. We can bisect this angle by bisecting ![]() and
and ![]() separately.
separately.
We proceed using complex numbers. Triangle ![]() is isosceles with side lengths
is isosceles with side lengths ![]() . The height of this from the base of
. The height of this from the base of ![]() is
is ![]() . Therefore, the complex number
. Therefore, the complex number ![]() represents the bisection of
represents the bisection of ![]() .
.
Similarly, using the 5-12-13 triangles, we easily see that ![]() represents the bisection of the angle
represents the bisection of the angle ![]() . Therefore, we can add these two angles together by multiplying the complex numbers, finding
. Therefore, we can add these two angles together by multiplying the complex numbers, finding
![]() Now the point
Now the point ![]() is given by the complex number
is given by the complex number ![]() . Therefore, to find a point on line
. Therefore, to find a point on line ![]() , we simply subtract
, we simply subtract ![]() , which is the same as multiplying
, which is the same as multiplying ![]() by the conjugate of
by the conjugate of ![]() . We find
. We find
![]() In particular, note that the tangent of the argument of this complex number is
In particular, note that the tangent of the argument of this complex number is ![]() , which must be the slope of the tangent line. Hence
, which must be the slope of the tangent line. Hence ![]() , and the answer is
, and the answer is ![]() .
.
Solution 3
We use the same reflection as in Solution 2. As ![]() , we know that
, we know that ![]() is isosceles. Hence
is isosceles. Hence ![]() . But by symmetry, we also know that
. But by symmetry, we also know that ![]() . Hence
. Hence ![]() . In particular, as
. In particular, as ![]() , this implies that
, this implies that ![]() , and
, and ![]() are concyclic.
are concyclic.
Let ![]() be the intersection of
be the intersection of ![]() with the
with the ![]() -axis. As
-axis. As ![]() is parallel to the
is parallel to the ![]() -axis, we know that
-axis, we know that ![]() But
But ![]() By the fact that
By the fact that ![]() is cyclic,
is cyclic, ![]() Therefore, combining (1), (2), and (3), we find that
Therefore, combining (1), (2), and (3), we find that
![]()
By symmetry, we also know that
![]() Therefore, (4) and (5) show by AA similarity that
Therefore, (4) and (5) show by AA similarity that ![]() . Therefore,
. Therefore, ![]() .
.
Now as ![]() , we know that
, we know that ![]() is isosceles, and as
is isosceles, and as ![]() , we can drop an altitude to
, we can drop an altitude to ![]() to easily find that
to easily find that ![]() . Therefore,
. Therefore, ![]() , which is the desired slope, must also be
, which is the desired slope, must also be ![]() . As before, we conclude that the answer is
. As before, we conclude that the answer is ![]() .
.
Solution 4
First, rewrite the equations for the circles as ![]() and
and ![]() .
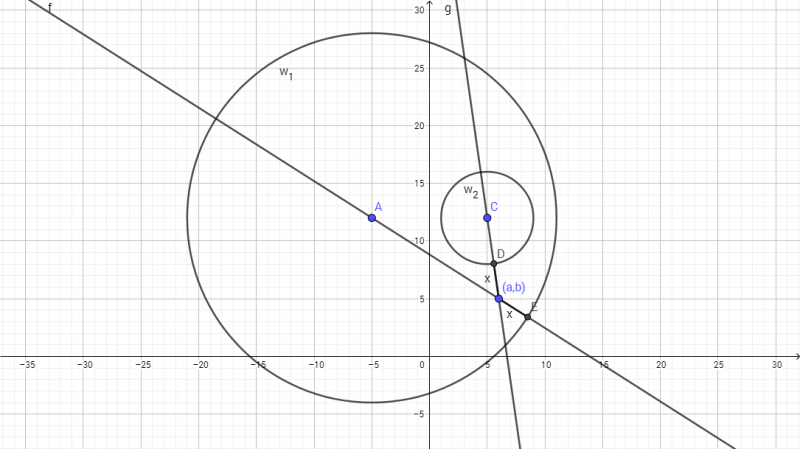
Then, choose a point
.
Then, choose a point ![]() that is a distance of
that is a distance of ![]() from both circles. Use the distance formula between
from both circles. Use the distance formula between ![]() and each of
and each of ![]() and
and ![]() (in the diagram above). The distances, as can be seen in the diagram above are
(in the diagram above). The distances, as can be seen in the diagram above are ![]() and
and ![]() , respectively.
, respectively.
![]()
![]() Subtracting the first equation from the second gives
Subtracting the first equation from the second gives ![]() Substituting this into the first equation gives
Substituting this into the first equation gives
![]()
![]() Now, instead of converting this to the equation of an eclipse, solve for
Now, instead of converting this to the equation of an eclipse, solve for ![]() and then divide by
and then divide by ![]() .
.
![]() We take the smaller root to minimize
We take the smaller root to minimize ![]() .
.
![]() Now, let
Now, let ![]() . This way,
. This way, ![]() .
Substitute this in.
.
Substitute this in. ![]() Then, take the derivative of this and set it to 0 to find the minimum value.
Then, take the derivative of this and set it to 0 to find the minimum value.
![]() Then, use this value of
Then, use this value of ![]() to find the minimum of
to find the minimum of ![]() to get
to get 
Solution 5 (probably fastest)
Like before, notice that the distances from the centers of the given circles to the desired center are ![]() and
and ![]() , which add up to
, which add up to ![]() . This means that the possible centers of the third circle lie on an ellipse with foci
. This means that the possible centers of the third circle lie on an ellipse with foci ![]() and
and ![]() . Using the fact that the sum of the distances from the foci is
. Using the fact that the sum of the distances from the foci is ![]() , we find that the semi-major axis has length
, we find that the semi-major axis has length ![]() and the semi-minor axis has length
and the semi-minor axis has length ![]() . Therefore, the equation of the ellipse is
. Therefore, the equation of the ellipse is ![]() where the numbers
where the numbers ![]() and
and ![]() come from
come from ![]() and
and ![]() respectively.
respectively.
We proceed to find ![]() using the same method as Solution 1.
using the same method as Solution 1.
Solution 6
First, obtain the equation of the ellipse as laid out in previous solutions. We now scale the coordinate plane in the ![]() direction by a factor of
direction by a factor of ![]() centered at
centered at ![]() This takes the ellipse to a circle centered at
This takes the ellipse to a circle centered at ![]() with radius
with radius ![]() and takes the line
and takes the line ![]() to
to  The tangent point of our line to the circle with positive slope forms a right triangle with the origin and the center of the circle. Thus, the distance from this tangent point to the origin is
The tangent point of our line to the circle with positive slope forms a right triangle with the origin and the center of the circle. Thus, the distance from this tangent point to the origin is ![]() By similar triangles, the slope of this line is then
By similar triangles, the slope of this line is then ![]() We multiply this by
We multiply this by ![]() to get
to get ![]() so our final answer is
so our final answer is ![]()
See also
| 2005 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.