2006 AMC 12A Problems/Problem 19

Problem

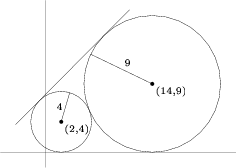
Circles with centers $(2,4)$ and $(14,9)$ have radii $4$ and $9$ , respectively. The equation of a common external tangent to the circles can be written in the form $y=mx+b$ with $m>0$ . What is $b$ ?

$\mathrm{(A) \ } \frac{908}{119}\qquad \mathrm{(B) \ } \frac{909}{119}\qquad \mathrm{(C) \ } \frac{130}{17}\qquad \mathrm{(D) \ } \frac{911}{119}\qquad \mathrm{(E) \ } \frac{912}{119}$

Solution

Let $L_1$ be the line that goes through $(2,4)$ and $(14,9)$ , and let $L_2$ be the line $y=mx+b$ . If we let $\theta$ be the measure of the acute angle formed by $L_1$ and the x-axis, then $\tan\theta=\frac{5}{12}$ . $L_1$ clearly bisects the angle formed by $L_2$ and the x-axis, so $m=\tan{2\theta}=\frac{2\tan\theta}{1-\tan^2{\theta}}=\frac{120}{119}$ . We also know that $L_1$ and $L_2$ intersect at a point on the x-axis. The equation of $L_1$ is $y=\frac{5}{12}x+\frac{19}{6}$ , so the coordinate of this point is $\left(-\frac{38}{5},0\right)$ . Hence the equation of $L_2$ is $y=\frac{120}{119}x+\frac{912}{119}$ , so $b=\frac{912}{119}$ , and our answer choice is $\boxed{\mathrm{E}}$ .

2006 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 18	Followed by Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

Page

Toolbox

Search

2006 AMC 12A Problems/Problem 19

Problem

Solution

See also