2011 AMC 12B Problems/Problem 20

Problem

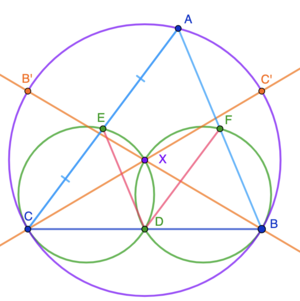
Triangle $ABC$ has $AB = 13, BC = 14$ , and $AC = 15$ . The points $D, E$ , and $F$ are the midpoints of $\overline{AB}, \overline{BC}$ , and $\overline{AC}$ respectively. Let $X \neq E$ be the intersection of the circumcircles of $\triangle BDE$ and $\triangle CEF$ . What is $XA + XB + XC$ ?

$\textbf{(A)}\ 24 \qquad \textbf{(B)}\ 14\sqrt{3} \qquad \textbf{(C)}\ \frac{195}{8} \qquad \textbf{(D)}\ \frac{129\sqrt{7}}{14} \qquad \textbf{(E)}\ \frac{69\sqrt{2}}{4}$

Solution 1 (Coordinates)

Let us also consider the circumcircle of $\triangle ADF$ .

Note that if we draw the perpendicular bisector of each side, we will have the circumcenter of $\triangle ABC$ which is $P$ , Also, since $m\angle ADP = m\angle AFP = 90^\circ$ . $ADPF$ is cyclic, similarly, $BDPE$ and $CEPF$ are also cyclic. With this, we know that the circumcircles of $\triangle ADF$ , $\triangle BDE$ and $\triangle CEF$ all intersect at $P$ , so $P$ is $X$ .

The question now becomes calculating the sum of the distance from each vertex to the circumcenter.

We can calculate the distances with coordinate geometry. (Note that $XA = XB = XC$ because $X$ is the circumcenter.)

Let $A = (5,12)$ , $B = (0,0)$ , $C = (14, 0)$ , $X= (x_0, y_0)$

Then $X$ is on the line $x = 7$ and also the line with slope $-\frac{5}{12}$ that passes through $(2.5, 6)$ .

$y_0 = 6-\frac{45}{24} = \frac{33}{8}$

So $X = (7, \frac{33}{8})$

and $XA +XB+XC = 3XB = 3\sqrt{7^2 + \left(\frac{33}{8}\right)^2} = 3\times\frac{65}{8}=\frac{195}{8}$

Solution 2 (Algebra)

Consider an additional circumcircle on $\triangle ADF$ . After drawing the diagram, it is noticed that each triangle has side values: $7$ , $\frac{15}{2}$ , $\frac{13}{2}$ . Thus they are congruent, and their respective circumcircles are.

Let $M$ & $N$ be $\triangle BDE$ & $\triangle CEF$ 's circumcircles' respective centers. Since $\triangle BDE$ & $\triangle CEF$ are congruent, the distance $M$ & $N$ each are from $\overline{BC}$ are equal, so $\overline{MN} || \overline{BC}$ . The angle between $\overline {MN}$ & $\overline{EX}$ is $90^{\circ}$ , and since $\overline{MN} || \overline{BC}$ , $\angle XEC$ is also $90^{\circ}$ . $\triangle XEC$ is a right triangle inscribed in a circle, so $\overline{XC}$ must be the diameter of $N$ . Using the same logic & reasoning, we could deduce that $XA$ & $XB$ are also circumdiameters.

Since the circumcircles are congruent, circumdiameters $XA$ , $XB$ , and $XC$ are congruent. Therefore, the solution can be found by calculating one of these circumdiameters and multiplying it by a factor of $3$ . We can find the circumradius quite easily with the formula $\sqrt{(s)(s-a)(s-b)(s-c)} = \frac{abc}{4R}$ , such that $s=\frac{a+b+c}{2}$ and $R$ is the circumradius. Since $s = \frac{21}{2}$ :

$\sqrt{(\frac{21}{2})(4)(3)(\frac{7}{2})} = \frac{\frac{15}{2}\cdot\frac{13}{2}\cdot 7}{4R}$

After a few algebraic manipulations:

$\Rightarrow R=\frac{65}{16} \Rightarrow XA = XB = XC = \frac{65}{8} \Rightarrow XA + XB + XC = \boxed{\frac{195}{8}}$ .

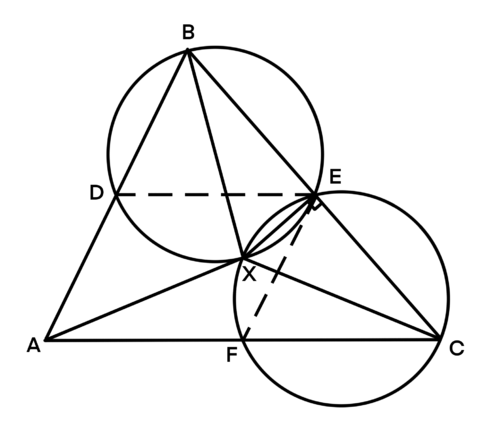
Solution 3 (Homothety)

Let $O$ be the circumcenter of $\triangle ABC,$ and $h_A$ denote the length of the altitude from $A.$ Note that a homothety centered at $B$ with ratio $\frac{1}{2}$ takes the circumcircle of $\triangle BAC$ to the circumcircle of $\triangle BDE$ . It also takes the point diametrically opposite $B$ on the circumcircle of $\triangle BAC$ to $O.$ Therefore, $O$ lies on the circumcircle of $\triangle BDE.$ Similarly, it lies on the circumcircle of $\triangle CEF.$ By Pythagorean triples, $h_A=12.$ Finally, our answer is $3R=3\cdot \frac{abc}{4\{ABC\}}=3\cdot \frac{abc}{2ah_A}=3\cdot \frac{bc}{2h_A}=\boxed{\frac{195}{8}.}$

Solution 4 (basically Solution 1 but without coordinates)

Since Solution 1 has already proven that the circumcenter of $\triangle ABC$ coincides with $X$ , we'll go from there. Note that the radius of the circumcenter of any given triangle is $\frac{a}{2\sin{A}}$ , and since $b=15$ and $\sin{B}=\frac{12}{13}$ , it can be easily seen that $XA = XB = XC = \frac{65}{8}$ and therefore our answer is $3\cdot \frac{65}{8}=\boxed{\frac{195}{8}}.$

Solution 5

Since $ED$ is a midline of $\triangle CAB,$ we have that $\triangle CED \sim \triangle CAB$ with a side length ratio of $1:2.$

Consider a homothety of scale factor $2$ with on $\triangle CED$ concerning point $C$ . Note that this sends $(CEDX)$ to $(ABCC')$ with $CX=XC'.$ By properties of homotheties, $C,X,$ and $C'$ are collinear. Similarly, we obtain that $BX=XB',$ with all three points collinear. Let $O$ denote the circumcenter of $\triangle ABC.$ It is well-known that $OX \perp CC'$ and analogously $OX \perp BB'.$ However, there is only one perpendicular line to $OX$ passing through $X,$ , therefore, $O$ coincides with $X.$

It follows that $AX=BX=CX=R,$ where $R$ is the circumradius of $\triangle ABC,$ and this can be computed using the formula $R=\frac{abc}{4[ABC]},$ from which we quickly obtain $R=\frac{65}{8} \implies AX+BX+CX=\boxed{\frac{195}{8}}.$

Solution 6 (Trigonometry)

$\angle BXE = \angle BDE$ , $\angle CXE = \angle CFE$ , as the angles are on the same circle.

$\triangle BDE \sim \triangle ABC$ , $\triangle CFE \sim \triangle ABC$

$\angle BDE = \angle A$ , $\angle CFE = \angle A$

$\angle BXE = \angle A$ , $\angle CXE = \angle A$

Therefore $\angle BXE = \angle CXE$ , and $XE$ is the angle bisector of $\triangle XBC$ . By the angle bisector theorem $\frac{XB}{XC} = \frac{BE}{CE} = 1$ , $XB = XC$ . In a similar fashion $XA = XB = XC = R$ , where $R$ is the circumcircle of $\triangle ABC$ .

By the law of cosine, $\cos A = \frac{13^2 + 15^2 - 14^2}{2 \cdot 13 \cdot 15} = \frac{33}{65}$ , $\sin A = \sqrt{1 - \left(\frac{33}{65}\right)^2} = \frac{56}{65}$

By the extended law of sines, $2R = \frac{BC}{\sin A} = \frac{14}{\frac{56}{65}} = \frac{65}{4}$ , $R = \frac{65}{8}$

$XA + XB + XC = 3 R = \boxed{\textbf{(C) } \frac{195}{8}}$

~isabelchen

2011 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 19	Followed by Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search