2020 AMC 10A Problems/Problem 20

The following problem is from both the 2020 AMC 12A #18 and 2020 AMC 10A #20, so both problems redirect to this page.

1 Problem
2 Solution 1
3 Solution 2 (Coordinates)
4 Solution 3 (Trigonometry)
5 Solution 4 (Law of Cosines)
6 Solution 5 (Vectors / Coordinates)
7 Solution 6 (Power of a Point)
8 Solution 7 (Solving Equations)
9 Solution 8
10 Solution 9 Trigonometry
11 Video Solution by Education, The Study of Everything
12 Video Solution by On The Spot STEM
13 Video Solution by MathEx
14 Video Solution by TheBeautyOfMath
15 Video Solution by Triviality
16 Video Solution by OmegaLearn
17 See Also

Problem

Quadrilateral $ABCD$ satisfies $\angle ABC = \angle ACD = 90^{\circ}, AC=20,$ and $CD=30.$ Diagonals $\overline{AC}$ and $\overline{BD}$ intersect at point $E,$ and $AE=5.$ What is the area of quadrilateral $ABCD?$

$\textbf{(A) } 330 \qquad \textbf{(B) } 340 \qquad \textbf{(C) } 350 \qquad \textbf{(D) } 360 \qquad \textbf{(E) } 370$

Solution 1

$[asy] size(15cm,0); import olympiad; draw((0,0)--(0,2)--(6,4)--(4,0)--cycle); label("A", (0,2), NW); label("B", (0,0), SW); label("C", (4,0), SE); label("D", (6,4), NE); label("E", (1.714,1.143), N); label("F", (1,1.5), N); draw((0,2)--(4,0), dashed); draw((0,0)--(6,4), dashed); draw((0,0)--(1,1.5), dashed); label("20", (0,2)--(4,0), SW); label("30", (4,0)--(6,4), SE); label("$x$", (1,1.5)--(1.714,1.143), NE); label("5$-$$x$", (1,1.5)--(0,2), NE); draw(rightanglemark((0,2),(0,0),(4,0))); draw(rightanglemark((0,2),(4,0),(6,4))); draw(rightanglemark((0,0),(1,1.5),(0,2))); [/asy]$

It's crucial to draw a good diagram for this one. Since $AC=20$ and $CD=30$ , we get $[ACD]=300$ . Now we need to find $[ABC]$ to get the area of the whole quadrilateral. Drop an altitude from $B$ to $AC$ and call the point of intersection $F$ . Let $FE=x$ . Since $AE=5$ , then $AF=5-x$ .

By dropping this altitude, we can also see two similar triangles, $\triangle BFE \sim \triangle DCE$ . Since $EC$ is $20-5=15$ , and $DC=30$ , we get that $BF=2x$ .

Now, if we redraw another diagram just of $ABC$ , we get that $(2x)^2=(5-x)(15+x)$ because of the altitude geometric mean theorem which states that in any right triangle, the altitude squared is equal to the product of the two lengths that it divides the base into.

Expanding, simplifying, and dividing by the GCF, we get $x^2+2x-15=0$ . This factors to $(x+5)(x-3)$ , which has roots of $x=-5, 3$ . Since lengths cannot be negative, $x=3$ . Since $x=3$ , that means the altitude $BF=2\cdot3=6$ , or $[ABC]=60$ . Thus $[ABCD]=[ACD]+[ABC]=300+60=\boxed {\textbf{(D) }360}$

~ Solution by Ultraman ~ Diagram by ciceronii

Solution 2 (Coordinates)

$[asy] size(10cm,0); draw((10,30)--(10,0)--(-8,-6)--(-10,0)--(10,30)); draw((-20,0)--(20,0)); draw((0,-15)--(0,35)); draw((10,30)--(-8,-6)); draw(circle((0,0),10)); label("E",(-4.05,-.25),S); label("D",(10,30),NE); label("C",(10,0),NE); label("B",(-8,-6),SW); label("A",(-10,0),NW); label("5",(-10,0)--(-5,0), NE); label("15",(-5,0)--(10,0), N); label("30",(10,0)--(10,30), E); dot((-5,0)); dot((-10,0)); dot((-8,-6)); dot((10,0)); dot((10,30)); [/asy]$ Let the points be $A(-10,0)$ , $\:B(x,y)$ , $\:C(10,0)$ , $\:D(10,30)$ ,and $\:E(-5,0)$ , respectively. Since $B$ lies on line $DE$ , we know that $y=2x+10$ . Furthermore, since $\angle{ABC}=90^\circ$ , $B$ lies on the circle with diameter $AC$ , so $x^2+y^2=100$ . Solving for $x$ and $y$ with these equations, we get the solutions $(0,10)$ and $(-8,-6)$ . We immediately discard the $(0,10)$ solution as $y$ should be negative. Thus, we conclude that $[ABCD]=[ACD]+[ABC]=\frac{20\cdot30}{2}+\frac{20\cdot6}{2}=\boxed{\textbf{(D)}\:360}$ .

Solution 3 (Trigonometry)

Let $\angle C = \angle{ACB}$ and $\angle{B} = \angle{CBE}.$ Using Law of Sines on $\triangle{BCE}$ we get $\dfrac{BE}{\sin{C}} = \dfrac{CE}{\sin{B}} = \dfrac{15}{\sin{B}}$ and LoS on $\triangle{ABE}$ yields $\dfrac{BE}{\sin{(90 - C)}} = \dfrac{5}{\sin{(90 - B)}} = \dfrac{BE}{\cos{C}} = \dfrac{5}{\cos{B}}.$ Divide the two to get $\tan{B} = 3 \tan{C}.$ Now, $\tan{\angle{CED}} = 2 = \tan{\angle{B} + \angle{C}} = \dfrac{4 \tan{C}}{1 - 3\tan^2{C}}$ and solve the quadratic, taking the positive solution (C is acute) to get $\tan{C} = \frac{1}{3}.$ So if $AB = a,$ then $BC = 3a$ and $[ABC] = \frac{3a^2}{2}.$ By Pythagorean Theorem, $10a^2 = 400 \iff \frac{3a^2}{2} = 60$ and the answer is $300 + 60 \iff \boxed{\textbf{(D)}}.$

(This solution is incomplete, can someone complete it please-Lingjun) ok Latex edited by kc5170

We could use the famous m-n rule in trigonometry in $\triangle ABC$ with Point $E$ [Unable to write it here.Could anybody write the expression] . We will find that $\overrightarrow{BD}$ is an angle bisector of $\triangle ABC$ (because we will get $\tan(x) = 1$ ). Therefore by converse of angle bisector theorem $AB:BC = 1:3$ . By using Pythagorean theorem, we have values of $AB$ and $AC$ . Computing $AB \cdot AC = 120$ . Adding the areas of $ABC$ and $ACD$ , hence the answer is $\boxed{\textbf{(D)}\:360}$ .

By: Math-Amaze

Latex: Catoptrics.

Solution 4 (Law of Cosines)

$[asy] import olympiad; pair A = (0, 189), B = (0,0), C = (570,0), D = (798, 798); dot("$A$", A, W); dot("$B$", B, S); dot("$C$", C, E); dot("$D$", D, N);dot("$E$",(140, 140), N); draw(A--B--C--D--A); draw(A--C, dotted); draw(B--D, dotted); [/asy]$

Denote $EB$ as $x$ . By the Law of Cosines: $AB^2 = 25 + x^2 - 10x\cos(\angle DEC)$ $BC^2 = 225 + x^2 + 30x\cos(\angle DEC)$

Adding these up yields: $400 = 250 + 2x^2 + 20x\cos(\angle DEC) \Longrightarrow x^2 + \frac{10x}{\sqrt{5}} - 75 = 0$ By the quadratic formula, $x = 3\sqrt5$ .

Observe: $[AEB] + [BEC] = \frac{1}{2}(x)(5)\sin(\angle DEC) + \frac{1}{2}(x)(15)\sin(180-\angle DEC) = (3)(20) = 60$ .

Thus the desired area is $\frac{1}{2}(30)(20) + 60 = \boxed{\textbf{(D) } 360}$

~qwertysri987

Solution 5 (Vectors / Coordinates)

Let $C = (0, 0)$ and $D = (0, 30)$ . Then $E = (-15, 0), A = (-20, 0),$ and $B$ lies on the line $y=2x+30.$ So the coordinates of $B$ are $(x, 2x+30).$

We can make this a vector problem. $\overrightarrow{\mathbf{B}} = \begin{pmatrix} x \\ 2x+30 \end{pmatrix}.$ We notice that point $B$ forms a right angle, meaning vectors $\overrightarrow{\mathbf{BC}}$ and $\overrightarrow{\mathbf{BA}}$ are orthogonal, and their dot-product is $0$ .

We determine $\overrightarrow{\mathbf{BC}}$ and $\overrightarrow{\mathbf{BA}}$ to be $\begin{pmatrix} -x \\ -2x-30 \end{pmatrix}$ and $\begin{pmatrix} -20-x \\ -2x-30 \end{pmatrix}$ , respectively. (To get this, we use the fact that $\overrightarrow{\mathbf{BC}} = \overrightarrow{\mathbf{C}}-\overrightarrow{\mathbf{B}}$ and similarly, $\overrightarrow{\mathbf{BA}} = \overrightarrow{\mathbf{A}} - \overrightarrow{\mathbf{B}}.$ )

Equating the cross-product to $0$ gets us the quadratic $-x(-20-x)+(-2x-30)(-2x-30)=0.$ The solutions are $x=-18, -10.$ Since $B$ clearly has a more negative x-coordinate than $E$ , we take $x=-18$ . So $B = (-18, -6).$

From here, there are multiple ways to get the area of $\Delta{ABC}$ to be $60$ , and since the area of $\Delta{ACD}$ is $300$ , we get our final answer to be $60 + 300 = \boxed{\text{(D) } 360}.$

-PureSwag

Solution 6 (Power of a Point)

$[asy] import olympiad; pair A = (0, 189), B = (0,0), C = (570,0), D = (798, 798),F=(285,94.5),G=(361.2,361.2); dot("$A$", A, W); dot("$B$", B, S); dot("$C$", C, E); dot("$D$", D, N);dot("$E$",(140, 140), N);dot("$F$",F,N);dot("$G$",G,N); draw(A--B--C--D--A); draw(A--C, dotted); draw(B--D, dotted); draw(F--G, dotted); [/asy]$

Let $F$ be the midpoint of $AC$ , and draw $FG // CD$ where $G$ is on $BD$ . We have $EF=5,FC=10$ .

$\Delta EFG \sim \Delta ECD \implies FG=10=FA=FC$ . Therefore $ABCG$ is a cyclic quadrilateral.

Notice that $\angle EFG=90^\circ, EG=\sqrt{5^2+10^2}=5\sqrt{5} \implies BE=\frac{AE\cdot EC}{EG}=\frac{5\cdot 15}{5\sqrt{5}}=3\sqrt{5}$ via Power of a Point.

The altitude from $B$ to $AC$ is then equal to $GF\cdot \frac{BE}{GE}=10\cdot \frac{3\sqrt 5}{5 \sqrt 5}=6$ .

Finally, the total area of $ABCD$ is equal to $\frac 12 \cdot 20 \left(30+6 \right) =\boxed{\text{(D) } 360}.$

~asops

Solution 7 (Solving Equations)

$[asy] size(15cm,0); import olympiad; draw((0,0)--(0,2)--(6,4)--(4,0)--cycle); label("A", (0,2), NW); label("B", (0,0), SW); label("C", (4,0), SE); label("D", (6,4), NE); label("E", (1.714,1.143), N); label("F", (1.714,0), SE); draw((0,2)--(4,0), dashed); draw((0,0)--(6,4), dashed); draw((1.714,1.143)--(1.714,0), dashed); label("20", (0,2)--(4,0), SW); label("30", (4,0)--(6,4), SE); label("$x$", (-0.3,2)--(-0.3,0), N); label("$y$", (0,-0.3)--(4,-0.3), E); draw(rightanglemark((1.714,2),(1.714,0),(5.714,0))); draw(rightanglemark((0,2),(0,0),(4,0))); draw(rightanglemark((0,2),(4,0),(6,4))); [/asy]$

Let $AB = x$ , $BC = y$

Looking at the diagram we have $x^2 + y^2 = 20^2$ , $DE = \sqrt{30^2+15^2} = 15\sqrt{5}$ , $[ACD] = \frac{1}{2} \cdot 20 \cdot 30 = 300$

Because $\triangle CEF \sim \triangle CAB$ , $EF = AB \cdot \frac{CE}{CA} = x \cdot \frac{15}{20} = \frac{3x}{4}$

$BF = BC - CF = BC - BC \cdot \frac{CE}{CA} = \frac{1}{4} \cdot BC = \frac{y}{4}$

$BE = \sqrt{ \left( \frac{3x}{4} \right) ^2 + \left( \frac{y}{4} \right) ^2 } = \frac{ \sqrt{9x^2 + y^2} }{4}$ , substituting $x^2 + y^2 = 400$ , we get $BE = \frac{ \sqrt{8x^2 + 400} }{4} = \frac{ \sqrt{2x^2 + 100} }{2}$

$[ABC] = \frac{1}{2} \cdot x \cdot y$

Because $\triangle ABC$ and $\triangle ACD$ share the same base, $\frac{[ABC]}{[ACD]} = \frac{BE}{DE}$

$[ABC] = [ACD] \cdot \frac{BE}{DE} = 300 \cdot \frac{ \frac{ \sqrt{2x^2 + 100} } {2} }{ 15 \sqrt{5} }$

$\frac{1}{2} \cdot x \cdot y = 20 \cdot \frac{ \frac{ \sqrt{2x^2 + 100} } {2} }{ \sqrt{5} }$

$xy = 4 \sqrt{10x^2 + 500}$

By $x^2 + y^2 = 400$ , $y = \sqrt{400 - x^2}$ . So, $x \cdot \sqrt{400 - x^2} = 4 \sqrt{10x^2 + 500}$

$x^2 (400 - x^2) = 16 (10x^2 + 500)$

Let $x^2 = a$ , $a (400 - a) = 16 (10a + 500)$ , $400a - a^2 = 160a + 8000$ , $a^2 - 240a + 8000 = 0$ , $(a-200)(a-40) = 0$

Because $x < 20$ , $a$ can only equal 40. $a = 40$ , $x = 2 \sqrt{10}$ , $y = 6 \sqrt{10}$

$[ABC] = \frac{1}{2} \cdot 2 \sqrt{10} \cdot 6 \sqrt{10} = 60$

$[ABCD] = [ABC] + [ACD] = 60 + 300 = \boxed{\text{(D) } 360}$

~isabelchen

Solution 8

Drop perpendiculars $\overline{AF}$ and $\overline{CG}$ to $\overline{BD}.$ Notice that since $\angle AEF=\angle CEG$ (since they are vertical angles) and $\angle AFE=\angle CGE=90^\circ,$ triangles $AEF$ and $CEG$ are similar. Therefore, we have

$x/EF=CE/AE=15/5=3,$

where $EG=x.$ Therefore, $EF=x/3.$

Additionally, angle chasing shows that triangles $CEG$ and $DCG$ are also similar. This gives $CG/x=DC/CE=30/15=2,$ so $CG=2x.$ Thus, applying the Pythagorean Theorem to triangle $CEG$ gives

$x^2+(2x)^2=15^2,$

so $EG=x=3\sqrt 5.$ Our pairs of similar triangles then allow us to fill in the following lengths (in this order):

$EF=x/3=\sqrt 5, CG=2x=6\sqrt 5, AF=CG/3=2\sqrt 5, DG=2\cdot CG=12\sqrt 5.$

Now, let $BF=y.$ Angle chasing shows that triangle $ABF$ and $BCG$ are similar, so $BG/AF=CG/BF.$ Plugging in known lengths gives

$\dfrac{y+4\sqrt 5}{2\sqrt 5}=\dfrac{6\sqrt 5}{y}.$

This gives $y=2\sqrt 5.$ Now we know all the lengths that make up $BD,$ which allows us to find

$BD=2\sqrt 5+\sqrt 5+3\sqrt 5+12\sqrt 5=18\sqrt 5.$

Therefore,

$\begin{align*} [ABCD] &= [ABD]+[CBD] \\ &= (BD)(AF)/2+(BD)(CG)/2 \\ &= (18\sqrt 5)(2\sqrt 5)/2+(18\sqrt 5)(6\sqrt 5)/2 \\ &= \boxed{\text{(D) } 360}. \end{align*}$

--vaporwave

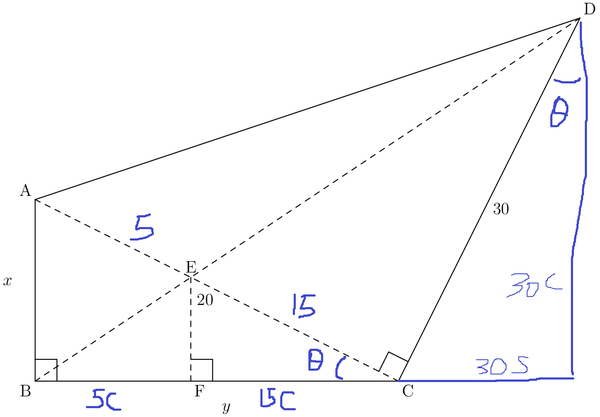
Solution 9 Trigonometry

set $\angle ACB = \theta , C= Cos(\theta), S = Sin(\theta)$

$E_y / E_x = 30C / ( 20C+30S) = 15S / (20C-15C)$

$2SC = 3/5$

$\begin{align*} [ABCD] &= [ABD]+[CBD] \\ &= 1/2*20C*30C + 1/2 * 20S (20C+30S) \\ &= 100* 2SC + 300 &= \boxed{\text{(D) } 360}. \end{align*}$

~luckuso

Video Solution by Education, The Study of Everything

https://youtu.be/5lb8kk1qbaA

Video Solution by On The Spot STEM

https://www.youtube.com/watch?v=hIdNde2Vln4

Video Solution by MathEx

https://www.youtube.com/watch?v=sHrjx968ZaM

Video Solution by TheBeautyOfMath

https://www.youtube.com/watch?v=RKlG6oZq9so

Video Solution by Triviality

https://youtu.be/R220vbM_my8?t=658 (amritvignesh0719062.0)

Video Solution by OmegaLearn

https://youtu.be/hDsoyvFWYxc?t=1224 ~ pi_is_3.14

2020 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 19	Followed by Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

2020 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 17	Followed by Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search