2021 AMC 12A Problems/Problem 24

1 Problem
2 Diagram
3 Solution 1 (Possible Without Trigonometry)
4 Solution 2 (Trigonometry)
5 Solution 3 (Weighted Averages and Similar Triangles)
6 Solution 4 (Similar Triangles)
7 Solution 5 (Law of Sine and Power of a Point)
8 Solution 6 (Analytic Geometry)
9 Video Solution by MOP 2024
10 Video Solution by Punxsutawney Phil
11 Video Solution by OmegaLearn (Similar Triangles, Law of Sines, Law of Cosines )
12 Video Solution
13 See also

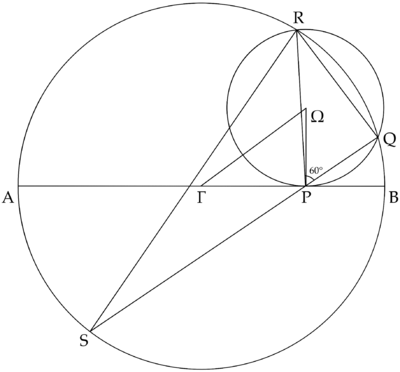
Problem

Semicircle $\Gamma$ has diameter $\overline{AB}$ of length $14$ . Circle $\Omega$ lies tangent to $\overline{AB}$ at a point $P$ and intersects $\Gamma$ at points $Q$ and $R$ . If $QR=3\sqrt3$ and $\angle QPR=60^\circ$ , then the area of $\triangle PQR$ equals $\tfrac{a\sqrt{b}}{c}$ , where $a$ and $c$ are relatively prime positive integers, and $b$ is a positive integer not divisible by the square of any prime. What is $a+b+c$ ?

$\textbf{(A) }110 \qquad \textbf{(B) }114 \qquad \textbf{(C) }118 \qquad \textbf{(D) }122\qquad \textbf{(E) }126$

Diagram

$[asy] /* Made by MRENTHUSIASM */ size(300); pair O, X, A, B, P, Q, R; O = (0,0); X = (4,3); A = (-7,0); B = (7,0); P = (4,0); Q = intersectionpoints(Circle(O,7),Circle(X,3))[0]; R = intersectionpoints(Circle(O,7),Circle(X,3))[1]; filldraw(P--Q--R--cycle,yellow); dot("$\Gamma$",O,S); dot("$\Omega$",X,E); dot("$A$",A,SW); dot("$B$",B,SE); dot("$P$",P,S); dot("$Q$",Q,E); dot("$R$",R,N); draw(arc(O, 7, 0, 180)^^A--B^^Circle(X,3)); [/asy]$ ~MRENTHUSIASM

Solution 1 (Possible Without Trigonometry)

Let $O=\Gamma$ be the center of the semicircle and $X=\Omega$ be the center of the circle.

Applying the Extended Law of Sines to $\triangle PQR,$ we find the radius of $\odot X:$ $XP=\frac{QR}{2\cdot\sin \angle QPR}=\frac{3\sqrt3}{2\cdot\frac{\sqrt3}{2}}=3.$ Alternatively, by the Inscribed Angle Theorem, $\triangle QRX$ is a $30^\circ\text{-}30^\circ\text{-}120^\circ$ triangle with base $QR=3\sqrt3.$ Dividing $\triangle QRX$ into two congruent $30^\circ\text{-}60^\circ\text{-}90^\circ$ triangles, we get that the radius of $\odot X$ is $XQ=XR=3$ by the side-length ratios.

Let $M$ be the midpoint of $\overline{QR}.$ By the Perpendicular Chord Bisector Converse, we have $\overline{OM}\perp\overline{QR}$ and $\overline{XM}\perp\overline{QR}.$ Together, points $O, X,$ and $M$ must be collinear.

By the SAS Congruence, we have $\triangle QXM\cong\triangle RXM,$ both of which are $30^\circ\text{-}60^\circ\text{-}90^\circ$ triangles. By the side-length ratios, we obtain $RM=\frac{3\sqrt3}{2}, RX=3,$ and $XM=\frac{3}{2}.$ By the Pythagorean Theorem on right $\triangle ORM,$ we get $OM=\frac{13}{2}$ and $OX=OM-XM=5.$ By the Pythagorean Theorem on right $\triangle OXP,$ we get $OP=4.$

Let $C$ be the foot of the perpendicular from $P$ to $\overline{QR},$ and $D$ be the foot of the perpendicular from $X$ to $\overline{PC},$ as shown below: $[asy] /* Made by MRENTHUSIASM */ size(300); pair O, X, A, B, P, Q, R, M, C, D; O = (0,0); X = (4,3); A = (-7,0); B = (7,0); P = (4,0); Q = intersectionpoints(Circle(O,7),Circle(X,3))[0]; R = intersectionpoints(Circle(O,7),Circle(X,3))[1]; M = midpoint(Q--R); C = foot(P,Q,R); D = foot(X,P,C); fill(P--Q--R--cycle,yellow); dot("$O$",O,S); dot("$X$",X,N); dot("$A$",A,SW); dot("$B$",B,SE); dot("$P$",P,S); dot("$Q$",Q,E); dot("$R$",R,N); dot("$M$",M,dir(M)); dot("$C$",C,NE); dot("$D$",D,SE); markscalefactor=0.0375; draw(rightanglemark(O,M,R),red); draw(rightanglemark(P,C,M),red); draw(rightanglemark(P,D,X),red); draw(rightanglemark(O,P,X),red); draw(P--Q--R--cycle); draw(arc(O, 7, 0, 180)^^A--B^^Circle(X,3)); draw(O--M^^X--P); draw(P--C^^X--D,dashed); [/asy]$ Clearly, quadrilateral $XDCM$ is a rectangle. Since $\angle XPD=\angle OXP$ by alternate interior angles, we have $\triangle XPD\sim\triangle OXP$ by the AA Similarity, with the ratio of similitude $\frac{XP}{OX}=\frac 35.$ Therefore, we get $PD=\frac 95$ and $PC=PD+DC=PD+XM=\frac 95 + \frac 32 = \frac{33}{10}.$

The area of $\triangle PQR$ is $\frac12\cdot QR\cdot PC=\frac12\cdot3\sqrt3\cdot\frac{33}{10}=\frac{99\sqrt3}{20},$ from which the answer is $99+3+20=\boxed{\textbf{(D) } 122}.$

~MRENTHUSIASM

Solution 2 (Trigonometry)

$[asy] size(150); draw(circle((7,0),7)); pair A = (0, 0); pair B = (14, 0); draw(A--B); draw(circle((11,3),3)); label("$C$", (7, 0), S); label("$O$", (11, 3), E); label("$P$", (11, 0), S); pair C = (7, 0); pair O = (11, 3); pair P = (11, 0); pair Q = intersectionpoints(circle(C, 7), circle(O, 3))[1]; pair R = intersectionpoints(circle(C, 7), circle(O, 3))[0]; draw(C--O); draw(C--Q); draw(C--R); draw(Q--R); draw(O--P); draw(O--Q); draw(O--R); draw(P--Q); draw(P--R); label("$Q$", Q, N); label("$R$", R, E); [/asy]$

Suppose we label the points as shown in the diagram above, where $C$ is the center of the semicircle and $O$ is the center of the circle tangent to $\overline{AB}$ . Since $\angle QPR = 60^{\circ}$ , we have $\angle QOR = 2\cdot 60^{\circ}=120^{\circ}$ and $\triangle QOR$ is a $30-30-120$ triangle, which can be split into two $30-60-90$ triangles by the altitude from $O$ . Since $QR=3\sqrt{3},$ we know $OQ=OR=\tfrac{3\sqrt{3}}{\sqrt{3}}=3$ by $30-60-90$ triangles. The area of this part of $\triangle PQR$ is $\frac{1}{2}bh=\tfrac{3\sqrt{3}}{2}\cdot\tfrac{3}{2}=\tfrac{9\sqrt{3}}{4}$ . We would like to add this value to the sum of the areas of the other two parts of $\triangle PQR$ .

To find the areas of the other two parts of $\triangle PQR$ using the $\sin$ area formula, we need the sides and included angles. Here we know the sides but what we don't know are the angles. So it seems like we will have to use an angle from another triangle and combine them with the angles we already know to find these angles easily. We know that $\angle QOR = 120^{\circ}$ and triangles $\triangle COQ$ and $\triangle COR$ are congruent as they share a side, $CQ=CR,$ and $OQ=OR$ . Therefore $\angle COQ = \angle COR = 120^{\circ}$ . Suppose $CO=x$ . Then $3^{2}+x^{2}-6x\cos{120^{\circ}}=7^{2}$ , and since $\cos{120^{\circ}}=-\tfrac{1}{2}$ , this simplifies to $x^{2}+3x=7^{2}-3^{2}\rightarrow x^{2}+3x-40=0$ . This factors nicely as $(x-5)(x+8)=0$ , so $x=5$ as $x$ can't be $-8$ . Since $CO=5, OP=3$ and $\angle OPC=90^{\circ}$ , we now know that $\triangle OPC$ is a $3-4-5$ right triangle. This may be useful info for later as we might use an angle in this triangle to find the areas of the other two parts of $\triangle PQR$ .

Let $\angle POC = \alpha$ . Then $\sin\alpha = \tfrac{4}{5}, \cos\alpha = \tfrac{3}{5}, \angle QOP = 120+\alpha,$ and $\angle POR = 120-\alpha$ . The sum of the areas of $\triangle QOP$ and $\triangle POR$ is $3\cdot 3\cdot\tfrac{1}{2}\cdot\left[\sin(120-\alpha)+\sin(120+\alpha)\right]=\tfrac{9}{2}\left[\sin(120-\alpha)+\sin(120+\alpha)\right],$ which we will add to $\tfrac{9\sqrt{3}}{4}$ to get the area of $\triangle PQR$ . Observe that $\sin(120-\alpha) = \sin 120\cos\alpha-\sin\alpha\cos 120 = \tfrac{\sqrt{3}}{2}\cdot\tfrac{3}{5}-\tfrac{4}{5}\cdot\tfrac{-1}{2}=\tfrac{3\sqrt{3}}{10}+\tfrac{4}{10}=\tfrac{3\sqrt{3}+4}{10}$ and similarly $\sin(120+\alpha)=\tfrac{3\sqrt{3}-4}{10}$ . Adding these two gives $\tfrac{3\sqrt{3}}{5}$ and multiplying that by $\tfrac{9}{2}$ gets us $\tfrac{27\sqrt{3}}{10},$ which we add to $\tfrac{9\sqrt{3}}{4}$ to get $\tfrac{54\sqrt{3}+45\sqrt{3}}{20}=\tfrac{99\sqrt{3}}{20}$ . The answer is $99+3+20=102+20=\boxed{\textbf{(D)} ~122}.$

~sugar_rush

Solution 3 (Weighted Averages and Similar Triangles)

$[asy] size(300); pair C = (7, 0); draw(arc(C, 7, 0, 180)); pair A = (0, 0), B = (14, 0); draw(A--B); draw(circle((11,3),3)); label("$A$", A, SSE); label("$B$", B, SSW); label("$C$", (A+B)/2, S); label("$O$", (11, 3), E); label("$P$", (11, 0), S); pair O = (11, 3), P = (11, 0), Q = intersectionpoints(circle(C, 7), circle(O, 3))[1], R = intersectionpoints(circle(C, 7), circle(O, 3))[0], S = (Q+R)/2, N = (121/8, 0), T = (8/11)*N + (3/11)*R, X = (4/7)*T + (3/7)*S; draw(C--O, blue); draw(O--S, red); draw(C--Q); draw(C--R); draw(Q--N--B); draw(O--P); draw(O--Q); draw(O--R); draw(P--Q--R--cycle); draw(B--T); draw(P--X); label("$Q$", Q, NNE); label("$R$", R, E); label("$S$", S, ENE); label("$N$", N, SSE); label("$T$", T, ENE); label("$X$", X, NE); draw(rightanglemark(P, X, Q)); draw(rightanglemark(B, T, R)); draw(rightanglemark(C, S, Q)); [/asy]$ Define points as shown above, where $N=\overleftrightarrow{PA}\cap\overleftrightarrow{QR}$ . The area of $\triangle PQR$ is simply $\dfrac{1}{2}PX\cdot QR=\dfrac{3\sqrt{3}}{2}PX;$ it remains to compute the value of $PX$ . Note that $PX$ is simply a weighted average of $BT$ and $CS;$ it is $\dfrac{CP}{BP}$ times closer to $BT$ than it is to $CS$ . Observe that $CS=\sqrt{CQ^{2}-\left(\dfrac{1}{2}QR\right)^{2}}=\sqrt{7^{2}-\left(\dfrac{3\sqrt{3}}{2}\right)^{2}}=6.5$ since the radius of $\Gamma$ is $7$ as its diameter is $14$ . Note also by the Extended Law of Sines the radius of $\Omega$ is $\dfrac{3\sqrt{3}}{2\sin 60^{\circ}}=3,$ so $OS=3\cos 60^{\circ}=1.5$ . Since $C, O,$ and $S$ are collinear by symmetry we have $CO=CS-OS=5,$ so $CP=\sqrt{5^{2}-3^{2}}=4$ and $BP=7-4=3$ . Therefore, $\triangle OPC$ is a $3\text{-}4\text{-}5$ right triangle; $\triangle OPC\sim\triangle NSC$ since $\angle OPC=\angle CSN=90^{\circ}$ and $\angle OCP=\angle NCS=\sin^{-1}\left(\dfrac{3}{5}\right)$ . Therefore $\dfrac{CN}{CS}=\cfrac{CO}{CP}=\dfrac{5}{4}$ so $CN=\dfrac{5}{4}CS=\dfrac{65}{8}$ . Since $\triangle BTN\sim\triangle CSN,$ we have $\dfrac{BT}{BN}=\dfrac{CS}{CN}=\dfrac{4}{5}$ . Therefore $BT=\dfrac{4}{5}BN=\dfrac{4}{5}\left(CN-7\right)=\dfrac{4}{5}\cdot\dfrac{9}{8}=\dfrac{36}{40}=0.9;$ so $PX$ is $\dfrac{4}{3}$ times as close to $0.9$ as to $6.5;$ we can compute $PX=\dfrac{4}{7}BT+\dfrac{3}{7}CS=\dfrac{4}{7}\cdot0.9+\dfrac{3}{7}\cdot6.5=3.3$ . The area of $\triangle PQR$ is $\dfrac{3\sqrt{3}}{2}\cdot 3.3=\dfrac{99\sqrt{3}}{20}$ and $99+3+20=\boxed{\textbf{(D)} ~122}$ .

~sugar_rush

Solution 4 (Similar Triangles)

Let $O_{1}$ be the center of $\odot\Gamma, O_2$ be the center of $\odot\Omega,$ and $M$ be the midpoint of $\overline{QR}.$ We have $O_{1}M=\sqrt{7^2-\left(\frac{3\sqrt3}{2}\right)^2}=\frac{13}{2}$ and by Extended Law of Sines, the radius of $\odot\Omega$ is $\frac{3\sqrt3}{2\sin 60^\circ}=3$ so $O_{2}M=3\cos 60^\circ=\frac{3}{2}.$ Therefore $O_{1}O_{2}=O_{1}M-O_{2}M=5$ and $O_{1}P=\sqrt{5^2 - 3^2}=4.$

Let $X=\overline{AB}\cap\overline{QR}.$ Obviously $\angle O_{1}PO_{2}=\angle O_{1}MX=90^\circ~\text{and}~\angle PO_{1}O_{2}=\angle MO_{1}X=\arcsin\left(\frac{3}{5}\right)$ so $\triangle PO_{1}O_{2}\sim\triangle MO_{1}X$ with ratio $\frac{PO_{1}}{MO_{1}}=\frac{4}{\tfrac{13}{2}}=\frac{8}{13}.$ Therefore $O_1X=\frac{13}{8}\cdot O_{1}O_{2}=\frac{13}{8}\cdot5=\frac{65}{8}$ and $MX=\frac{13}{8}\cdot PO_{2}=\frac{13}{8}\cdot3=\frac{39}{8}.$

Let $H$ denote the foot of the altitude from $P$ to $\overline{QR}.$ Because $\overline{PH}\parallel\overline{O_{1}M},$ it follows that $\triangle PHX\sim\triangle O_{1}MX.$ This similarity has ratio $\frac{PX}{O_{1}X}=1-\frac{O_{1}P}{O_{1}X}=1-\frac{4}{\tfrac{65}{8}}=1-\frac{32}{65}=\frac{33}{65}.$ We therefore have $PH=\frac{33}{65}\cdot O_{1}M=\frac{33}{65}\cdot\frac{13}{2}=\frac{33}{10}.$

Finally, the area of $\triangle PQR$ is $\frac{1}{2}\cdot QR\cdot PH=\frac{1}{2}\cdot3\sqrt3\cdot\frac{33}{10}=\frac{99\sqrt3}{20},$ so the answer is $99+3+20=\boxed{\textbf{(D)}~122}.$

~inventivedant

Solution 5 (Law of Sine and Power of a Point)

By the Law of Sine in $\triangle PQR$ and its circumcircle $\odot \Omega$ , $2r_{\Omega} = \frac{QR}{ \sin 60^{\circ} } = \frac{ 3\sqrt{3} }{ \frac{ \sqrt{3} }{2} } = 6$ , $r_{\Omega} = 3$

$\Gamma \Omega = \sqrt{r_{\Gamma}^2 - \left( \frac{ PQ }{2}\right)^2} - \sqrt{r_{\Omega}^2 - \left( \frac{PQ}{2}\right)^2} = \sqrt{7^2 - \left( \frac{ 3 \sqrt{3} }{2}\right)^2} - \sqrt{3^2 - \left( \frac{ 3 \sqrt{3} }{2}\right)^2} = \frac{13}{2} - \frac32 = 5, \quad \Gamma P = \sqrt{5^2 - 3^2} = 4$

By Power of a Point in $\odot \Gamma$ , $PQ \cdot PS = PA \cdot PB = (7+4)(7-4) = 33$ .

By the Law of Sine in $\triangle PRS$ , $\frac{PR}{PS} = \frac{ \sin \angle PSR }{ \sin \angle PRS }$

By the Law of Sine in $\triangle QRS$ and its circumcircle $\odot \Gamma$ , $\frac{QR}{ \sin \angle PSR } = 14$ , $\frac{ 3\sqrt{3} }{ \sin \angle PSR } = 14$ , $\sin \angle PSR = \frac{ 3\sqrt{3} }{14}$ , $\cos \angle PSR = \frac{ 13 }{14}$

$\sin \angle PRS = \sin ( 60^{\circ} - \angle PSR ) = \sin 60^{\circ} \cos \angle PSR - \sin \angle PSR \cos 60^{\circ} = \frac{ \sqrt{3} }{2} \cdot \frac{ 13 }{14} - \frac{ 3\sqrt{3} }{14} \cdot \frac12 = \frac{ 5\sqrt{3} }{14}$

$\frac{PR}{PS} = \frac{ \frac{ 3\sqrt{3} }{14} }{ \frac{ 5\sqrt{3} }{14} } = \frac35, \quad PQ \cdot PR = PQ \cdot PS \cdot \frac{PR}{PS} = 33 \cdot \frac35 = \frac{99}{5}$

$[PQR] = \frac12 \cdot \sin 60^{\circ} \cdot PQ \cdot PR = \frac12 \cdot \frac12 \cdot \frac{99}{5} = \frac{ 99\sqrt{3} }{20}, \quad 99 + 3 + 20 = \boxed{\textbf{(D)}~122}$

~isabelchen

Solution 6 (Analytic Geometry)

Following Solution 4, We have $O_{1}$ (0,0) , $O_{2}$ (4,3). We can write the equation of the two circles as: $\odot\Gamma : x^{2}+y^{2}=7^{2}...(1)$ $\odot\Omega : (x-4)^{2}+(y-3)^{2}=3^{2}...(2)$ By substituting (1) into (2), we get $8x+6y-65=0...(3)$ Notice (3) is the relationship between $x$ value and $y$ value, in other words, (3) is the linear equation that go through $R$ and $Q$ . Let the height drops from $P$ to $QR$ at $H$ . Therefore, we have $Area \triangle PQR =\frac{1}{2}\cdot{QR}\cdot{PH}$ So $QR=3\sqrt{3}$ And by distance formula, $PH$ is the distance from $P$ (4,0) to $\overline{QR}$ . $PH={\frac{|8\cdot4+6\cdot0-65|}{\sqrt{8^{2}+6^{2}}}=\frac{33}{10}}$ Thus, We get $Area \triangle PQR =\frac{1}{2}\cdot3\sqrt{3}\cdot\frac{33}{10}=\frac{99\sqrt{3}}{20}$ So the answer is $99+3+20=\boxed{\textbf{(D)}~122}.$

~ERiccc

Video Solution by MOP 2024

https://youtube.com/watch?v=UJ_M_cjul1Q

~r00tsOfUnity

Video Solution by Punxsutawney Phil

https://youtube.com/watch?v=cEHF5iWMe9c

This is invalid. ~r00tsOfUnity

Video Solution by OmegaLearn (Similar Triangles, Law of Sines, Law of Cosines )

https://youtu.be/j965v6ahUZk

~pi_is_3.14

Video Solution

https://youtu.be/VUvSH-8AxzM

~MathProblemSolvingSkills.com

2021 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 23	Followed by Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search