2016 USAMO Problems/Problem 3
Contents
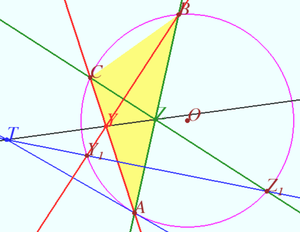
Problem
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its
denote its ![]() -excenter,
-excenter, ![]() -excenter, and circumcenter, respectively. Points
-excenter, and circumcenter, respectively. Points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]() Similarly, points
Similarly, points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]()
Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]() and
and ![]() are perpendicular.
are perpendicular.
Solution
This problem can be proved in the following two steps.
1. Let ![]() be the
be the ![]() -excenter, then
-excenter, then ![]() and
and ![]() are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for
are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for ![]()
2. Show that ![]() which implies
which implies ![]() This can be proved by multiple applications of the Pythagorean Thm.
This can be proved by multiple applications of the Pythagorean Thm.
Solution 2
We find point ![]() on line
on line ![]() we prove that
we prove that ![]() and state that
and state that ![]() is the point
is the point ![]() from ENCYCLOPEDIA OF TRIANGLE, therefore
from ENCYCLOPEDIA OF TRIANGLE, therefore ![]()
Let ![]() be circumcircle of
be circumcircle of ![]() centered at
centered at ![]() Let
Let ![]() and
and ![]() be crosspoints of
be crosspoints of ![]() and
and ![]() and
and ![]() respectively.
Let
respectively.
Let ![]() be crosspoint of
be crosspoint of ![]() and
and ![]() In accordance the Pascal theorem for pentagon
In accordance the Pascal theorem for pentagon ![]()
![]() is tangent to
is tangent to ![]() at
at ![]()
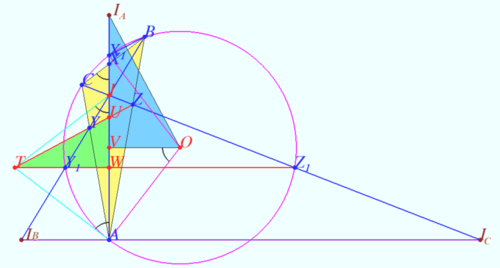
Let ![]() be
be ![]() and
and ![]() -excenters of
-excenters of ![]() Denote
Denote ![]()
![]()
![]()
![]() is the foot ot perpendicular from
is the foot ot perpendicular from ![]() to
to ![]()
![]() is ortocenter of
is ortocenter of ![]() and incenter of
and incenter of ![]()
![]() is the Nine–point circle of
is the Nine–point circle of ![]()
![]() is the midpoint of
is the midpoint of ![]() is the midpoint of
is the midpoint of ![]() in accordance with property of Nine–point circle
in accordance with property of Nine–point circle ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() In
In ![]() segment
segment ![]() cross segment
cross segment ![]() where
where ![]()
![]()
![]()
![]()
![]()
![]()
![]()
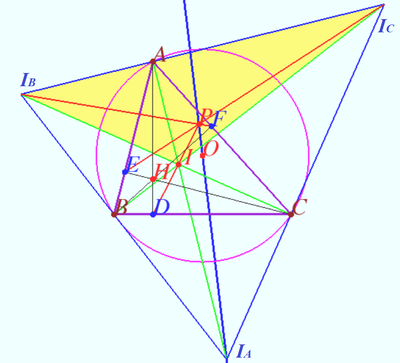
Let ![]() be the base triangle with orthocenter
be the base triangle with orthocenter ![]() center of Nine-points circle
center of Nine-points circle ![]() be the Euler line of
be the Euler line of ![]()
![]() is orthic triangle of
is orthic triangle of ![]()
![]() is orthic-of-orthic triangle.
is orthic-of-orthic triangle.
![]() is perspector of base triangle and orthic-of-orthic triangle.
is perspector of base triangle and orthic-of-orthic triangle.
Therefore ![]() is point
is point ![]() of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
[[1]]
of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
[[1]]
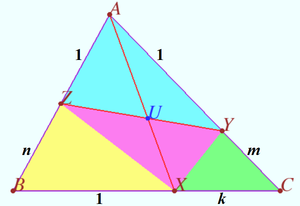
Claim ![]() Proof
Proof
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See also
| 2016 USAMO (Problems • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.