Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2011 AIME II Problems/Problem 4

Problem 4

In triangle $ABC$, $AB=20$ and $AC=11$. The angle bisector of $\angle A$ intersects $BC$ at point $D$, and point $M$ is the midpoint of $AD$. Let $P$ be the point of the intersection of $AC$ and $BM$. The ratio of $CP$ to $PA$ can be expressed in the form $\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Solution 1

[asy] pointpen = black; pathpen = linewidth(0.7); pair A = (0,0), C= (11,0), B=IP(CR(A,20),CR(C,18)), D = IP(B--C,CR(B,20/31*abs(B-C))), M = (A+D)/2, P = IP(M--2*M-B, A--C), D2 = IP(D--D+P-B, A--C); D(MP("A",D(A))--MP("B",D(B),N)--MP("C",D(C))--cycle); D(A--MP("D",D(D),NE)--MP("D'",D(D2))); D(B--MP("P",D(P))); D(MP("M",M,NW)); MP("20",(B+D)/2,ENE); MP("11",(C+D)/2,ENE); [/asy] Let $D'$ be on $\overline{AC}$ such that $BP \parallel DD'$. It follows that $\triangle BPC \sim \triangle DD'C$, so \[\frac{PC}{D'C} = 1 + \frac{BD}{DC} = 1 + \frac{AB}{AC} = \frac{31}{11}\] by the Angle Bisector Theorem. Similarly, we see by the Midline Theorem that $AP = PD'$. Thus, \[\frac{CP}{PA} = \frac{1}{\frac{PD'}{PC}} = \frac{1}{1 - \frac{D'C}{PC}} = \frac{31}{20},\] and $m+n = \boxed{51}$.

Solution 2 (mass points)

Assign mass points as follows: by Angle-Bisector Theorem, $BD / DC = 20/11$, so we assign $m(B) = 11, m(C) = 20, m(D) = 31$. Since $AM = MD$, then $m(A) = 31$, and $\frac{CP}{PA} = \frac{m(A) }{ m(C)} = \frac{31}{20}$, so $m+n = \boxed{51}$.

Solution 3

By Menelaus' Theorem on $\triangle ACD$ with transversal $PB$, \[1 = \frac{CP}{PA} \cdot \frac{AM}{MD} \cdot \frac{DB}{CB} = \frac{CP}{PA} \cdot \left(\frac{1}{1+\frac{AC}{AB}}\right) \quad \Longrightarrow \quad \frac{CP}{PA} = \frac{31}{20}.\] So $m+n = \boxed{051}$.

Solution 4

We will use barycentric coordinates. Let $A = (1, 0, 0)$, $B = (0, 1, 0)$, $C = (0, 0, 1)$. By the Angle Bisector Theorem, $D = [0:11:20] = \left(0, \frac{11}{31}, \frac{20}{31}\right)$. Since $M$ is the midpoint of $AD$, $M = \frac{A + D}{2} = \left(\frac{1}{2}, \frac{11}{62}, \frac{10}{31}\right)$. Therefore, the equation for line BM is $20x = 31z$. Let $P = (x, 0, 1-x)$. Using the equation for $BM$, we get \[20x = 31(1-x)\] \[x = \frac{31}{51}\] Therefore, $\frac{CP}{PA} = \frac{1-x}{x} = \frac{31}{20}$ so the answer is $\boxed{051}$.

Solution 5

Let $DC=x$. Then by the Angle Bisector Theorem, $BD=\frac{20}{11}x$. By the Ratio Lemma, we have that $\frac{PC}{AP}=\frac{\frac{31}{11}x\sin\angle PBC}{20\sin\angle ABP}.$ Notice that $[\triangle BAM]=[\triangle BMD]$ since their bases have the same length and they share a height. By the sin area formula, we have that \[\frac{1}{2}\cdot20\cdot BM\cdot \sin\angle ABP=\frac{1}{2}\cdot \frac{20}{11}x\cdot BM\cdot\sin\angle PBC.\] Simplifying, we get that $\frac{\sin\angle PBC}{\sin\angle ABP}=\frac{11}{x}.$ Plugging this into what we got from the Ratio Lemma, we have that $\frac{PC}{AP}=\frac{31}{20}\implies\boxed{051.}$

Solution 6 (quick Menelaus)

First, we will find $\frac{MP}{BP}$. By Menelaus on $\triangle BDM$ and the line $AC$, we have \[\frac{BC}{CD}\cdot\frac{DA}{AM}\cdot\frac{MP}{PB}=1\implies \frac{62MP}{11BP}=1\implies \frac{MP}{BP}=\frac{11}{62}.\] This implies that $\frac{MB}{BP}=1-\frac{MP}{BP}=\frac{51}{62}$. Then, by Menelaus on $\triangle AMP$ and line $BC$, we have \[\frac{AD}{DM}\cdot\frac{MB}{BP}\cdot\frac{PC}{CA}=1\implies \frac{PC}{CA}=\frac{31}{51}.\] Therefore, $\frac{PC}{AP}=\frac{31}{51-31}=\frac{31}{20}.$ The answer is $\boxed{051}$. -brainiacmaniac31

Solution 7 (Visual)

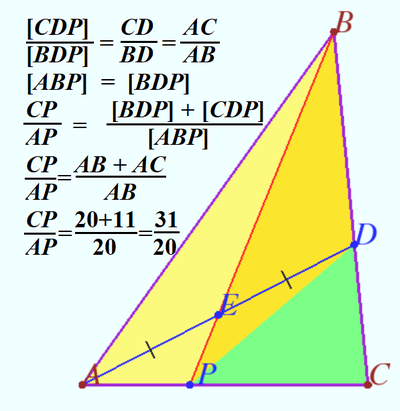2011 AIME II 4.png vladimir.shelomovskii@gmail.com, vvsss


Solution 8 (Cheese)

Assume $ABC$ is a right triangle at $A$. Line $AD = x$ and $BC = \tfrac{-11}{20}x + 11$. These two lines intersect at $D$ which have coordinates $(\frac{220}{31},\frac{220}{31})$ and thus $M$ has coordinates $(\frac{110}{31},\frac{110}{31})$. Thus, the line $BM = \tfrac{11}{51} \cdot (20-x)$. When $x = 0$, $P$ has $y$ coordinate equal to $\frac{11\cdot20}{51} \frac{AP + CP}{AP} = 1 + \frac{CP}{AP}$ = $\tfrac{51}{20} = 1 + \frac{CP}{AP},$ which equals ${\tfrac{31}{20}},$ giving an answer of $\boxed{51}.$

Solution 9 (Menelaus + Ceva's + Angle Bisector Theorem)

We start by using Menelaus' theorem on $\triangle ABD$ and $EC$. So, we see that $\frac{BC}{DC}\cdot\frac{DM}{AM}\cdot\frac{AE}{EB}=1$. By Angle Bisector theorem, $\frac{BC}{DC}=\frac{31}{11}$, and therefore after plugging in our values we get $\frac{AE}{EB}=\frac{11}{31}$. Then, by Ceva's on the whole figure, we have $\frac{CP}{PA}\cdot\frac{AE}{EB}\cdot\frac{BD}{DC}=1$. Plugging in our values, we get $\frac{CP}{PA}=\frac{31}{20}$, giving an answer of $\boxed{51}$. ~ESAOPS

Video Solution by OmegaLearn

https://youtu.be/Gjt25jRiFns?t=314

~ pi_is_3.14

See also

2011 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2011_AIME_II_Problems/Problem_4&oldid=210760"