Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2021 USAMO Problems/Problem 6

Problem 6

Let $ABCDEF$ be a convex hexagon satisfying $\overline{AB} \parallel \overline{DE}$, $\overline{BC} \parallel \overline{EF}$, $\overline{CD} \parallel \overline{FA}$, and\[AB \cdot DE = BC \cdot EF = CD \cdot FA.\]Let $X$, $Y$, and $Z$ be the midpoints of $\overline{AD}$, $\overline{BE}$, and $\overline{CF}$. Prove that the circumcenter of $\triangle ACE$, the circumcenter of $\triangle BDF$, and the orthocenter of $\triangle XYZ$ are collinear.

Solution 1

Let $M_1$, $M_2$, and $M_3$ be the midpoints of $CE$, $AE$, $AC$ and $N_1$, $N_2$, and $N_3$ be the midpoints of $DF$, $BF$, and $BD$. Also, let $H$ be the orthocenter of $XYZ$. Note that we can use parallel sides to see that $X$, $Z$, and $M_3$ are collinear. Thus we have \[\text{Pow}(M_3,(XYZ)) = M_3Z \cdot M_3X = \frac 14 AB \cdot DE\] by midlines. Applying this argument cyclically, and noting the condition $AB \cdot DE = BC \cdot EF = CD \cdot FA$, $M_1$, $M_2$, $M_3$, $N_1$, $N_2$, $N_3$ all lie on a circle concentric with $(XYZ)$.

Next, realize that basic orthocenter properties imply that the circumcenter $O_1$ of $(ACE)$ is the orthocenter of $\triangle M_1M_2M_3$, and likewise the circumcenter $O_2$ of $(BDF)$ is the orthocenter of $\triangle N_1N_2N_3$.

The rest is just complex numbers; toss on the complex plane so that the circumcenter of $\triangle XYZ$ is the origin. Then we have \[o_1 = m_1+m_2+m_3 = (c+e)/2+(a+e)/2+(a+c)/2=a+c+e\] \[o_2 = n_1+n_2+n_3 = (b+d)/2+(d+f)/2+(b+f)/2=b+d+f\] \[h = x+y+z = (a+d)/2+(b+e)/2+(c+f)/2=(a+b+c+d+e+f)/2.\] Note that from the above we have $h=\frac{o_1+o_2}{2}$, so $H$ is the midpoint of segment $O_1O_2$. In particular, $H$, $O_1$, and $O_2$ are collinear, as required.

~ Leo.Euler

Solution 2

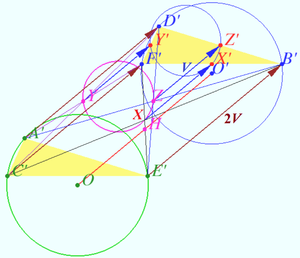
2021 USAMO 6b.png
2021 USAMO 6c.png
2021 USAMO 6a.png

We construct two equal triangles, prove that triangle $XYZ$ is the same as medial triangle of both this triangles. We use property of medial triangle and prove that circumcenters of constructed triangles coincide with given circumcenters.

Denote $A' = C + E – D, B' = D + F – E, C' = A+ E – F,$ $D' = F+ B – A, E' = A + C – B, F' = B+ D – C.$ Then $A' – D' = C + E – D – ( F+ B – A) = (A + C + E ) – (B+ D + F).$

Denote $D' – A' = 2\vec V.$

Similarly we get $B' – E' = F' – C' = D' – A' \implies$ $\triangle A'C'E' = \triangle D'F'B'.$

The translation vector maps $\triangle A'C'E'$ into $\triangle D'F'B'$ is $2\vec {V.}$ $X = \frac {A+D}{2} = \frac { (A+ E – F) + (D + F – E)}{2} = \frac {C' + B'}{2} = \frac {E' + F'}{2},$

so $X$ is midpoint of $AD, B'C',$ and $E'F'.$ Symilarly $Y$ is the midpoint of $BE, A'F',$ and $C'D', Z$ is the midpoint of $CF, A'B',$ and $D'E'.$ $Z + V = \frac {A' + B'}{2}+ \frac {D' – A'}{2} = \frac {B' + D'}{2} = Z'$ is the midpoint of $B'D'.$

Similarly $X' = X + V$ is the midpoint of $B'F',Y'= Y + V$ is the midpoint of $D'F'.$

Therefore $\triangle X'Y'Z'$ is the medial triangle of $\triangle B'D'F'.$

$\triangle XYZ$ is $\triangle X'Y'Z'$ translated on $– \vec {V}.$

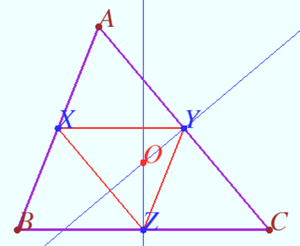
It is known (see diagram) that circumcenter of triangle coincide with orthocenter of the medial triangle. Therefore orthocenter $H$ of $\triangle XYZ$ is circumcenter of $\triangle B'D'F'$ translated on $– \vec {V}.$

It is the midpoint of segment $OO'$ connected circumcenters of $\triangle B'D'F'$ and $\triangle A'C'E'.$

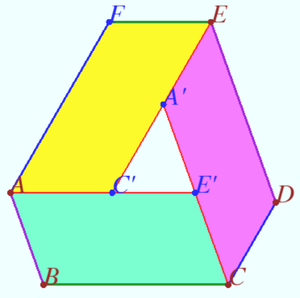
According to the definition of points $A', C', E',$ quadrangles $ABCE', CDEA',$ and $AFEC'$ are parallelograms. Hence \[AC' = FE, AE' = BC, CE' = AB, CA' = DE, EA' = CD, EC' = AF \implies\] \[AC' \cdot AE' = CE' \cdot CA' = EA' \cdot EC' = AB \cdot DE \implies\] Power of points A,C, and E with respect circumcircle $\triangle A'C'E'$ is equal, hence distances between these points and circumcenter of $\triangle A'C'E'$ are the same. Therefore circumcenter $\triangle ACE$ coincide with circumcenter $\triangle A'C'E'.$

Similarly circumcenter of $\triangle BDF$ coincide with circumcenter of $\triangle B'D'F'.$

vladimir.shelomovskii@gmail.com, vvsss

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_USAMO_Problems/Problem_6&oldid=193415"