2008 iTest Problems/Problem 96

Problem

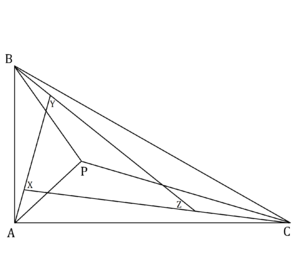
Triangle $ABC$ has $\angle A=90^\circ, \angle B=60^\circ$ , and $AB=8$ , and a point $P$ is chosen inside the triangle. The interior angle bisectors $\ell_A, \ell_B$ , and $\ell_C$ of respective angles $PAB, PBC$ , and $PCA$ intersect pairwise at $X=\ell_A\cap\ell_C, Y=\ell_A\cap\ell_B$ , and $Z=\ell_B\cap\ell_C$ . If triangles $ABC$ and $XYZ$ are directly similar, then the area of $\triangle XYZ$ may be written in the form $\tfrac{p\sqrt q-r\sqrt s}t$ , where $p,q,r,s,t$ are positive integers, $q$ and $s$ are not divisible by the square of any prime, and $\gcd(t,r,p)=1$ . Compute $p+q+r+s+t$ .

Solution

Let $x = \angle BAY$ . With some angle chasing, we find that $\angle PBC = \angle PCA = 2x$ , $\angle APC = 90^\circ$ , $\angle APB = 120^\circ$ , and $\angle BPC = 150^\circ$ .

By using 30-60-90 triangles, we find that $AC = 8\sqrt{3}$ and $BC = 16$ . By the Law of Sines on $\triangle APB$ and $\triangle BPC$ , $\tfrac{8}{\frac{\sqrt{3}}{2}} = \tfrac{BP}{\sin(2x)}$ and $\tfrac{BP}{\sin(30-2x)} = \tfrac{16}{\frac12}$ . After solving for $BP$ in both equations, we have $\begin{align*} \frac{16}{\sqrt{3}} \sin(2x) &= 32 \left( \frac12 \cos(2x) - \frac{\sqrt{3}}{2} \sin(2x) \right) \\ \frac{\sin(2x)}{\sqrt{3}} &= \cos(2x) - \sqrt{3} \sin(2x) \\ \frac{4\sqrt{3}}{3} \left( \sin(2x) \right) &= \cos(2x) \\ \tan(2x) &= \frac{\sqrt{3}}{4}. \end{align*}$ Thus, by using identities, $\sin(x) = \sqrt{\frac{19 - 4\sqrt{19}}{19}}$ . Now we will determine the length of $XZ$ . We will only substitute $\sin(x)$ at the very end (along with the other trigonometric expressions) to keep calculations simple.

Using the definition of a cosine, we have $XC = 8\sqrt{3} \cos(x)$ . By the Law of Sines on $\triangle BZC$ , $\tfrac{16}{\frac12} = \tfrac{ZC}{\sin(x)}$ , so $ZC = 32 \sin(x)$ . Thus $XZ = 8\sqrt{3} \cos(x) - 32 \sin(x)$ .

We know that the area of $\triangle ABC$ is $32\sqrt{3}$ and that $XZ/AC = \frac{8\sqrt{3} \cos(x) - 32 \sin(x)}{8\sqrt{3}}.$ Therefore, $\begin{align*} [XYZ] &= 32\sqrt{3} \cdot \frac{64 \cdot 3 \cos^2 (x) - 16 \cdot 32\sqrt{3} \sin(x) \cos(x) + 32^2 \sin^2 (x)}{64 \cdot 3} \\ &= \sqrt{3} \left( \frac{96 \cos^2 (x) - 256\sqrt{3} \sin(x) \cos(x) + 32 \cdot 16 \sin^2 (x)}{3} \right) \\ &= 16\sqrt{3} \left( \frac{26 \sin^2 (x) - 8\sqrt{3} \sin(2x) + 6}{3} \right) \\ &= 16\sqrt{3} \left( \frac{26(\frac{19-4\sqrt{19}}{38}) - 8\sqrt{3} \frac{\sqrt{3}}{\sqrt{19}} + 6}{3} \right) \\ &= \frac{16\sqrt{3}}{3} \left( 13 - \frac{52\sqrt{19}}{19} - \frac{24\sqrt{19}}{19} + 6 \right) \\ &= \frac{16\sqrt{3}}{3} ( 19 - 4\sqrt{19} ) \\ &= \frac{304\sqrt{3} - 64\sqrt{57}}{3} \end{align*}$ Therefore, $p+q+r+s+t = \boxed{431}$ .

Note

The original problem says that $X=\ell_A\cap\ell_B, Y=\ell_B\cap\ell_C$ , and $Z=\ell_C\cap\ell_A$ . This is a typo.

2008 iTest (Problems)
Preceded by: Problem 95	Followed by: Problem 97
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40 • 41 • 42 • 43 • 44 • 45 • 46 • 47 • 48 • 49 • 50 • 51 • 52 • 53 • 54 • 55 • 56 • 57 • 58 • 59 • 60 • 61 • 62 • 63 • 64 • 65 • 66 • 67 • 68 • 69 • 70 • 71 • 72 • 73 • 74 • 75 • 76 • 77 • 78 • 79 • 80 • 81 • 82 • 83 • 84 • 85 • 86 • 87 • 88 • 89 • 90 • 91 • 92 • 93 • 94 • 95 • 96 • 97 • 98 • 99 • 100

Page

Toolbox

Search

2008 iTest Problems/Problem 96

Contents

Problem

Solution

Note

See Also