Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2012 AMC 10A Problems/Problem 21

Problem

Let points $A$ = $(0 ,0 ,0)$, $B$ = $(1, 0, 0)$, $C$ = $(0, 2, 0)$, and $D$ = $(0, 0, 3)$. Points $E$, $F$, $G$, and $H$ are midpoints of line segments $\overline{BD},\text{ } \overline{AB}, \text{ } \overline {AC},$ and $\overline{DC}$ respectively. What is the area of $EFGH$?

$\textbf{(A)}\ \sqrt{2}\qquad\textbf{(B)}\ \frac{2\sqrt{5}}{3}\qquad\textbf{(C)}\ \frac{3\sqrt{5}}{4}\qquad\textbf{(D)}\ \sqrt{3}\qquad\textbf{(E)}\ \frac{2\sqrt{7}}{3}$

Solution 1

Consider a tetrahedron with vertices at $A,B,C,D$ on the $xyz$-plane. The length of $EF$ is just one-half of $AD$ because it is the midsegment of $\triangle ABD.$ The same concept applies to the other side lengths. $AD=3$ and $BC=\sqrt{1^2+2^2}=\sqrt{5}$. Then $EF=HG=\frac32$ and $EH=FG=\frac{\sqrt{5}}{2}$. The line segments lie on perpendicular planes so quadrilateral $EFGH$ is a rectangle. The area is

\[EF \cdot FG = \frac 32 \cdot \frac{\sqrt{5}}{2} = \frac{3\sqrt 5} 4\implies \boxed{\textbf C}.\]

[asy] import three; draw((0,0,0)--(1,0,0)--(0,0,3)--cycle); draw((0,0,0)--(0,2,0)); draw((0,2,0)--(0,0,3)); //EFGH draw((0.5,0,1.5)--(0.5,0,0)--(0,1,0)--(0,1,1.5)--(0.5,0,1.5),red); //Points label("$E$",(0.5,0,1.5),NW); label("$F$",(0.5,0,0),S); label("$G$",(0,1,0),S); label("$H$",(0,1,1.5),NE); label("$A$",(0,0,0),NE); label("$B$",(1,0,0),S); label("$C$",(0,2,0),S); label("$D$",(0,0,3),N); [/asy]

Solution 2

Computing the points of $EFGH$ gives $E(0.5, 0, 1.5), F(0.5, 0, 0), G(0,1,0), H(0,1,1.5)$. The vector $EF$ is $(0,0,-1.5)$, while the vector $HG$ is also $(0,0,-1.5)$, meaning the two sides $EF$ and $GH$ are parallel. Similarly, the vector $FG$ is $(-0.5, 1, 0)$, while the vector $EH$ is also $(-0.5, 1, 0)$. Again, these are equal in both magnitude and direction, so $FG$ and $EH$ are parallel. Thus, figure $EFGH$ is a parallelogram.

Computation of vectors $EF$ and $HG$ is sufficient evidence that the figure is a parallelogram, since the vectors are not only point in the same direction, but are of the same magnitude, but the other vector $FG$ is needed to find the angle between the sides.

Taking the dot product of vector $EF$ and vector $FG$ gives $0 \cdot -0.5 + 0 \cdot 1 + -1.5 \cdot 0 = 0$, which means the two vectors are perpendicular. (Alternately, as above, note that vector $EF$ goes directly down on the z-axis, while vector $FG$ has no z-component and lie completely in the xy plane.) Thus, the figure is a parallelogram with a right angle, which makes it a rectangle. 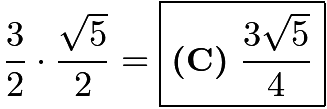With the distance formula in three dimensions, we find that $EF = \frac{3}{2}$ and $FG = \frac{\sqrt{5}}{2}$, giving an area of $\frac32 \cdot \frac{\sqrt{5}}{2} = \boxed{\textbf{(C)}\ \frac{3\sqrt{5}}{4}}$

Video Solution by Richard Rusczyk

https://artofproblemsolving.com/videos/amc/2012amc10a/249

~dolphin7

See Also

2012 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2012_AMC_10A_Problems/Problem_21&oldid=175516"