2023 AMC 12A Problems/Problem 24

Problem

Let $K$ be the number of sequences $A_1$ , $A_2$ , $\dots$ , $A_n$ such that $n$ is a positive integer less than or equal to $10$ , each $A_i$ is a subset of $\{1, 2, 3, \dots, 10\}$ , and $A_{i-1}$ is a subset of $A_i$ for each $i$ between $2$ and $n$ , inclusive. For example, $\{\}$ , $\{5, 7\}$ , $\{2, 5, 7\}$ , $\{2, 5, 7\}$ , $\{2, 5, 6, 7, 9\}$ is one such sequence, with $n = 5$ .What is the remainder when $K$ is divided by $10$ ?

$\textbf{(A) } 1 \qquad \textbf{(B) } 3 \qquad \textbf{(C) } 5 \qquad \textbf{(D) } 7 \qquad \textbf{(E) } 9$

Solution 1

Consider any sequence with $n$ terms. Every 10 number has such choices: never appear, appear the first time in the first spot, appear the first time in the second spot… and appear the first time in the $n$ th spot, which means every number has $(n+1)$ choices to show up in the sequence. Consequently, for each sequence with length $n$ , there are $(n+1)^{10}$ possible ways.

Thus, the desired value is 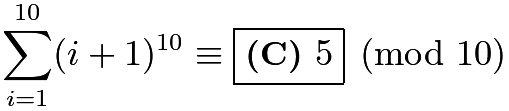$\sum_{i=1}^{10}(i+1)^{10}\equiv \boxed{\textbf{(C) } 5}\pmod{10}$

~bluesoul

Solution 2

Let $f(x,\ell)$ be the number of sequences $A_1$ , $A_2$ , $\dots$ , $A_\ell$ such that each $A_i$ is a subset of $\{1, 2,\dots,x\}$ , and $A_i$ is a subset of $A_{i+1}$ for $i=1$ , $2\dots$ , $\ell-1$ . Then $f(x,1)=2^x$ and $f(0,\ell)=1$ .

If $\ell\ge2$ and $x\ge1$ , we need to get a recursive formula for $f(x,\ell)$ : If $|A_1|=i$ , then $A_1$ has $\text C_x^i$ possibilities, and the subsequence $\{A_i\}_{2\le i\le\ell}$ has $f(x-i,\ell-1)$ possibilities. Hence $f(x,\ell)=\sum_{i=0}^x\text C_x^if(x-i,\ell-1).$ By applying this formula and only considering modulo $10$ , we get $f(1,2)=3$ , $f(1,3)=4$ , $f(1,4)=5$ , $f(1,5)=6$ , $f(1,6)=7$ , $f(1,7)=8$ , $f(1,8)=9$ , $f(1,9)=0$ , $f(1,10)=1$ , $f(2,2)=9$ , $f(2,3)=6$ , $f(2,4)=5$ , $f(2,5)=6$ , $f(2,6)=9$ , $f(2,7)=4$ , $f(2,8)=1$ , $f(2,9)=0$ , $f(2,10)=1$ , $f(3,2)=7$ , $f(3,3)=4$ , $f(3,4)=5$ , $f(3,5)=6$ , $f(3,6)=3$ , $f(3,7)=2$ , $f(3,8)=9$ , $f(3,9)=0$ , $f(3,10)=1$ , $f(4,2)=1$ , $f(4,3)=6$ , $f(4,4)=5$ , $f(4,5)=6$ , $f(4,6)=1$ , $f(4,7)=6$ , $f(4,8)=1$ , $f(4,9)=0$ , $f(4,10)=1$ , $f(5,2)=3$ , $f(5,3)=4$ , $f(5,4)=5$ , $f(5,5)=6$ , $f(5,6)=7$ , $f(5,7)=8$ , $f(5,8)=9$ , $f(5,9)=0$ , $f(5,10)=1$ , $f(6,2)=9$ , $f(6,3)=6$ , $f(6,4)=5$ , $f(6,5)=6$ , $f(6,6)=9$ , $f(6,7)=4$ , $f(6,8)=1$ , $f(6,9)=0$ , $f(6,10)=1$ , $f(7,2)=7$ , $f(7,3)=4$ , $f(7,4)=5$ , $f(7,5)=6$ , $f(7,6)=3$ , $f(7,7)=2$ , $f(7,8)=9$ , $f(7,9)=0$ , $f(7,10)=1$ , $f(8,2)=1$ , $f(8,3)=6$ , $f(8,4)=5$ , $f(8,5)=6$ , $f(8,6)=1$ , $f(8,7)=6$ , $f(8,8)=1$ , $f(8,9)=0$ , $f(8,10)=1$ , $f(9,2)=3$ , $f(9,3)=4$ , $f(9,4)=5$ , $f(9,5)=6$ , $f(9,6)=7$ , $f(9,7)=8$ , $f(9,8)=9$ , $f(9,9)=0$ , $f(9,10)=1$ , $f(10,2)=9$ , $f(10,3)=6$ , $f(10,4)=5$ , $f(10,5)=6$ , $f(10,6)=9$ , $f(10,7)=4$ , $f(10,8)=1$ , $f(10,9)=0$ , $f(10,10)=1$ .

Lastly, we get $K\equiv\textstyle\sum\limits_{i=1}^{10}f(10,i)\equiv\boxed{\textbf{(C) } 5}\pmod{10}$ . ~Quantum-Phantom

Solution 3 (Cheese, but this time it actually works)

Seeing that all the answers are different modulus 5, and that 10 is divisible by 5, we cheese this problem.

Let $A_1, A_2, \cdots, A_n$ be one sequence satisfying the constraints of the problem. Let $b_1, b_2, \cdots, b_n, b_{n+1}$ be the sequence of nonnegative integers such that $A_k$ has $b_k$ elements for all $1\leq{}k\leq{}n$ , and $b_{n+1}=10$ . Note that we can generate the number of valid sequences of $A$ by first generating all sequences of $b$ such that $b_i\leq{}b_{i+1}$ for all $1\leq{}i<n$ , then choosing the elements from $A_{k+1}$ that we keep in $A_k$ , given the sequence of $b$ as the restraint for the number of elements. 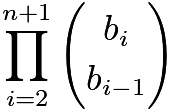For each sequence $b_1, b_2, \cdots{}, b_{n+1}$ , there are $\prod_{i=2}^{n+1}\binom{b_i}{b_{i-1}}$ corresponding sequences for $A$ . Now, consider two cases - either all terms in $b$ are either 0, 5, or 10, or there is at least one term in $b$ that is neither 0, 5 nor 10. In the second case, consider the last term in $b$ that is not 10 or 5, say $b_m$ . 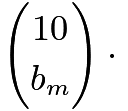However, that implies $b_{m+1}=10$ , and so the number of corresponding sequences of $A$ is $\binom{10}{b_m}\cdot{}$ something or 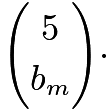$\binom{5}{b_m}\cdot$ something, which is always a multiple of $5$ . Therefore, we only need to consider sequences of $b$ where each term is $0$ $5$ or $10$ . If all terms in $b$ are 0 or 10, then for each $1\leq{}n\leq{}10$ there are $n+1$ sequences of $b$ (since there are $n+1$ places to turn from $0$ to $10$ ), for a total of $2+3+\cdots+11=65\equiv0$ (mod 5). If there exists at least one term $b_k=5$ , then we use stars and bars to count the number of sequences of $b$ , and each sequence of $b$ corresponds to $\binom{10}{5}$ sequences of $A$ . For each $n$ , we must have at least one term of $5$ . 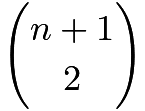After that, there are $n-1$ stars and $2$ bars (separating $0$ to $5$ and $5$ to $10$ ), so that is $\binom{n+1}{2}$ sequences of $b$ . 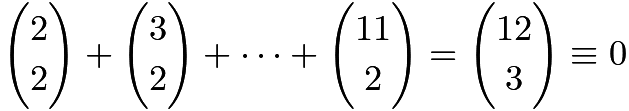So the sum is $\binom{2}{2}+\binom{3}{2}+\cdots+\binom{11}{2}=\binom{12}{3}\equiv0$ (mod 5). Therefore, the answer is 0 mod 5, and it must be $\boxed{\textbf{(C) } 5}$

Solution

We observe that in each sequence, if element $e \in A_i$ , then $e \in A_j$ for all $j \geq i$ . Therefore, to determine a sequence with a fixed length $n$ , we only need to determine the first set $A_i$ that each element in $\left\{ 1, 2, \cdots , 10 \right\}$ is inserted into, or an element is never inserted into any subset.

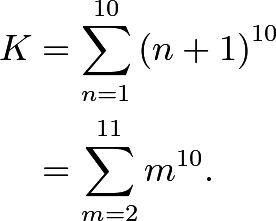
We have $\begin{align*} K & = \sum_{n = 1}^{10} \left( n + 1 \right)^{10} \\ & = \sum_{m = 2}^{11} m^{10} . \end{align*}$

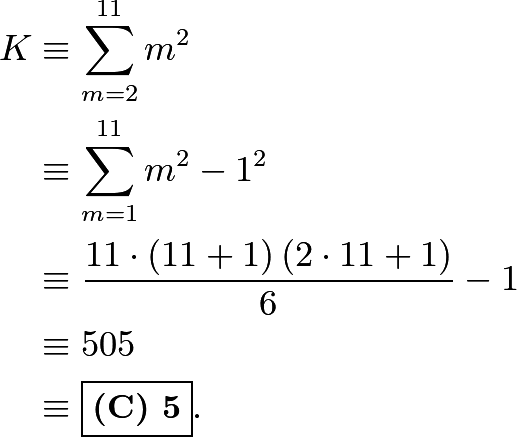
Recalling or noticing that $x^n \equiv x^{n \mod 4} \pmod {10}$ , then, Modulo 10, we have $\begin{align*} K & \equiv \sum_{m = 2}^{11} m^2 \\ & \equiv \sum_{m = 1}^{11} m^2 - 1^2 \\ & \equiv \frac{11 \cdot \left( 11 + 1 \right) \left( 2 \cdot 11 + 1 \right)}{6} - 1\\ & \equiv 505 \\ & \equiv \boxed{\textbf{(C) 5}} . \end{align*}$

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Slightly easier, observe that $11^{10} \equiv 1^{10 }\pmod {10}$ , so, working ${\mod 10}$ , we have

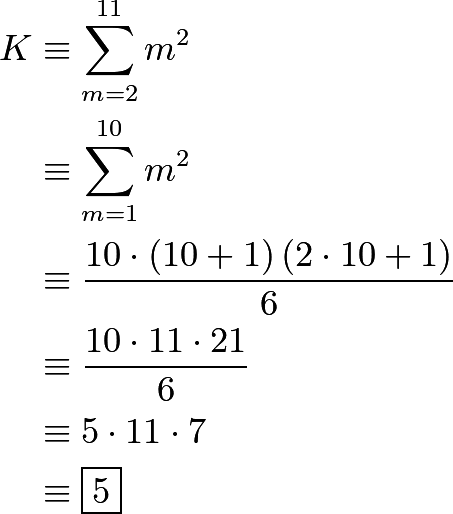
$\begin{align*} K & \equiv \sum_{m = 2}^{11} m^2 \\ & \equiv \sum_{m = 1}^{10} m^2 \\ & \equiv \frac{10 \cdot \left( 10 + 1 \right) \left( 2 \cdot 10 + 1 \right)}{6} \\ & \equiv \frac{10 \cdot 11 \cdot 21}{6} \\ & \equiv 5 \cdot 11 \cdot 7 \\ & \equiv \boxed{ 5} \end{align*}$

~oinava

Video Solution 1 by OmegaLearn

https://youtu.be/0LLQW0XCKsQ

Video Solution

https://youtu.be/FpagLq1uzBI

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

2023 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 23	Followed by Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search