ou’ve figured out the solution to the problem — fantastic! But you’re not finished. Whether you are writing solutions for a competition, a journal, a message board, or just to show off for your friends, you must master the art of communicating your solution clearly.

Brilliant ideas and innovative solutions to problems are pretty worthless if you can’t communicate them. In this article, we explore many aspects of how to write a clear solution. Below is an index; each page of the article includes a sample ‘How Not To’ solution and ‘How To’ solution. One common theme you’ll find throughout each point is that every time you make an experienced reader have to think to follow your solution, you lose.

As you read the ‘How To’ solutions, you may think some of them are overwritten. Indeed, some of them could be condensed. Some steps we chose to prove could probably be cited without proof. However, it is far better to prove too much too clearly than to prove too little. Rarely will a reader complain that a solution is too easy to understand or too easy on the eye.

One note of warning: many of the problems we use for examples are extremely challenging problems. Beginners, and even intermediate students, should not be upset if they have difficulty solving the problems on their own.

Table of Contents:

• Have a Plan
• Readers Are Not Interpreters
• U s e S p a c e
• sdrawkcaB knihT, Write Forwards
• Name Your Characters
• A Picture is Worth a Thousand Words
• Solution Readers, Not Mind Readers
• Follow the Lemmas
• Clear Casework
• Proofreed
• Bookends

‍

Your goal in writing a clear solution is to prevent the reader from having to think. You must express your ideas clearly and concisely. The experienced reader should never have to wonder where you are headed, or why any claim you make is true. The first step in writing a clear solution is having a plan. Make a simple outline of your solution. Include the items you’ll need to define, and the order in which you will write up the important parts of your solution. The outline will help ensure that you don’t skip anything and that you put your steps in an order that’s easy to follow.

Here’s a sample problem:

A sphere of radius 𝑟 is inscribed in a tetrahedron. Planes tangent to this sphere and parallel to the faces of the tetrahedron cut off four small tetrahedra from the tetrahedron; these small tetrahedra have inscribed spheres with radii 𝑎, 𝑏, 𝑐, 𝑑. Show that:

𝑎+𝑏+𝑐+𝑑=2𝑟

Here’s a solution that looks short but is pretty tough to read.

How Not to Write the Solution:

(General solution method found by community member zabelman in the Olympiad Geometry class.)

The main problem with the above solution is one of organization. We defined variables after they popped up. Midway through the solution we sidetracked to prove the volume of ABCD is 𝑟𝑆/3. Sometimes we wrote important equations right in our paragraphs instead of highlighting them by giving them their own lines.

If we outline before writing the solution, we won’t have these problems. We can list what we need to define, decide what items we need to prove before our main proof (we call these lemmas), and list the important steps so we know what to highlight.

Our scratch sheet with the outline might have the following:

Stuff to define: 𝐴𝐵𝐶𝐷,ℎ𝑎,𝑆,[𝐴],𝐴𝑋𝑌𝑍.

Order of things to prove:

‍

This list looks obvious once you have it written up, but if you just plow ahead with the solution without planning, you may end up skipping items and having to wedge them in as we did in our ‘How Not to Write the Solution’.

How to Write the Solution:

(General solution method found by community member zabelman in the Olympiad Geometry class.)

‍

The first thing a reader sees on your paper isn’t the structure of your solution. It isn’t the answer, it isn’t the words you choose. It’s how the solution sits on the paper. If the reader has to decipher scrawl, you’re going to lose him. Ideally, you’ll typeset your solution with a program like LaTeX. However, in most contests you don’t have the luxury of turning to a computer and you’ll have to write it out by hand. There are few very important rules of thumb when writing a solution by hand. Many are obvious, some are less so. You should follow them all.

1. Use blank paper. Don’t use graph paper or lined paper – the lines often make solutions harder to read. Never use paper that is torn out of a spiral notebook.
2. Respect margins. If you are starting with a completely blank piece of paper, draw the margins on all four sides (top, bottom, right, left). Make your margins at least 0.5 inches, and preferably a full inch.
3. Write horizontally; never turn your writing when you reach the end of a line in order to jam in a little more information. You can always start a new line or a new page.
4. Leave space at the top for a ‘Page _ of _’ so the reader knows how many pages there are, and what page she’s on. You probably won’t know how many pages you’ll write when you start, but you can fill these out when you’re finished. If you get to the bottom of a page and your solution must continue on another page, write ‘Continued’ at the bottom of that page so the reader knows we’re not finished. (This also helps readers know if they’re missing pages.)
5. Don’t write in cursive. Print. And print clearly.
6. Use pen. If you must use pencil, do not erase – the smudges from erasers make a mess.
7. When you make a mistake you’d like to omit, draw a single line through it and move on. If it’s a large block to omit, draw an ‘X’ through it and move on. Don’t scribble out large blocks of text.
8. If you left something out and want to add it at the end, put a simple symbol, like a (*), at the point where you would like the new text to be considered added, and leave a brief note, such as ‘Proof below.’ Below, you can write ‘(*) Addendum:’ and proceed with the proof. Don’t use a bunch of arrows to direct the reader all over the page.

Below are two solutions. Neither solution is picture-perfect; when you’re under time pressure, it’s hard to write perfect-looking proofs. You should find the second one much more enjoyable to read. When you’re writing solutions, keep the above tips in mind, and just remember, ‘If they can’t read it, it’s not right.’

How Not to Write the Solution:

That solution above is a mess. The one below took me just as long to write, and is much easier to read.

How to Write the Solution:

‍

imagineyoutrytoreadaparagraphoftextthathasnopuncuationnocapitalsandjustenough
spaceinittobreakuplinessoitdoesntmessupbrowsersitsreallytoughtoreadandpretty
soonyoulldecidethatitsnotworthreadingandyoullgoandreadsomethingelseyouwont
realizehowterriblyharditistotypelikethisitshardbecausewhenyoureusedtowritingcle
arlyandusingspaceandpunctuationandsentencestructureitgetsreallyhardtowritewith
outitsimilarlyonceyougetusedtoproperlyusingspaceinwritingyoursolutionsitwillbesec
ondnatureandyoullactuallyfindithardtowriteanindecipherableproof

When you write your solution you should:

1. Give each important definition or equation its own line.
2. Don’t bury too much algebra in a paragraph. You can write line after line of algebra, but put each step on its own line. Don’t cram the algebra in a paragraph.
3. Label equations or formulas or lemmas or cases you will use later very clearly.
4. Remember that there’s always more paper.

‍

Have fun reading this solution.

How Not to Write the Solution:

Here’s the same solution, with nearly the same wording.

How to Write the Solution:

Which would you rather read?

‍

The following is an excerpt from a cookbook that was never written:

“Figuring out how to make an omelette is easy. Anybody who has eaten an omelette knows that an omelette is typically made with several eggs filled with various foods such as ham, peppers, onions, and bacon and is often cooked with cheese. The fact that all these ingredients end up inside the egg means that we should begin cooking the eggs flatly on a pan and then add the ingredients. We can then roll part of the egg over the ingredients so as to trap them on the inside. If we needed some of the ingredients precooked we could do that before adding them to the eggs…”

It is one thing to figure out how to make an omelette. It is another to explain to somebody else how to make one. Starting our explanation from the beginning is much clearer than starting with the finished omelette.

“Prepare vegetables and other desired omelette fillings. Beat eggs. Start cooking the eggs. Add your fillings in the middle so that part of the egg can be pulled over the ingredients. When the omelette is closed, continue to cook and flip the omelette until the eggs look well-cooked.”

The reader doesn’t care how the process of cooking an omelette was unraveled by the author. The reader just wants to know how to make an omelette.

Think of solutions as recipes. Start at the beginning and move forward. List the ingredients and explain how and when to add them to the pot.

Here’s a sample problem.

This solution might be a good way to see how we might come up with a solution from scratch, but it’s not a particularly well-written proof:

How Not to Write the Solution:

The cookbook style is easier to read and far more convincing.

How to Write the Solution:

‍

A large thin-shelled vehicle for a young fowl that was created by a huge female bird sat on a wall. The large thin-shelled vehicle for a young fowl that was created by a huge female bird had a great fall. All the horses of the great man who lived in a large castle that ruled over the people in the land and all the men of the great man who lived in a large castle that ruled over the people in the land couldn’t put the large thin-shelled vehicle for a young fowl that was created by a huge female bird back together again.

Proofs are a lot like stories. When writing a solution your job is tell a math story in a way your audience will understand and enjoy. Instead of writing about ‘A large thin-shelled vehicle for a young fowl that was created by a huge female bird,’ we call that big egg ‘Humpty-Dumpty’ and tell the story. Likewise, a well-written proof often involves naming the important quantities or ideas that play a part in the story of your solution. Naming your characters can also help you find solutions to problems, so it’s not something you should wait until proof-writing time to do.

When you do name your characters, you name them simply, clearly, and write up front, so the reader knows exactly where to go to find out exactly who this 𝑛 person is and what that 𝑓(𝑥) function stands for.

Here’s an example problem.

The solution below is hard to read because the integers and the sums that are the key to the solution remain unnamed.

How Not to Write the Solution:

The solution below is easy to read because the main characters have names. Specifically, we name the integers in the set and the sums of the elements in subsets that we examine. These names allow us to follow the characters throughout the story. They also allow the writer to describe the characters more completely and succinctly.

How to Write the Solution:

When you’re writing a solution to a geometry problem, or any problem involving a picture, you should include the diagram. If you don’t include the diagram, you often make the grader have to draw it for you. Even if the diagram is given in the problem, you should include it in your solution. If you make your reader go looking somewhere else for a diagram, you are very likely to lose their attention.

Draw your diagram precisely. Use a geometry rendering program if you are typesetting your solution, or use a ruler and compass if you are writing your solution by hand.

Here’s an example.

Here’s a solution without a diagram.

How to Write the Solution:

(Solution method found by community member 3cnfsat in the Olympiad Geometry class)

Here’s a solution that includes the diagram:

How to Write the Solution:

(Solution method found by community member 3cnfsat in the Olympiad Geometry class)

If you aren’t familiar with this fact, try to prove it yourself (and write a nice solution). Every good geometer reaches for this fact as easily as they reach for the Pythagorean Theorem.

A full solution does not just mean a correct answer. You should justify every notable step of your solution. An experienced reader should never wonder ‘Why is that true?’ while reading your solution. She should also never be left in doubt as to whether or not you know why it is true.

It’s not always clear what steps you can assume the reader understands and what steps you have to explain. Here are a few guidelines:

‍

Here is a sample problem:

(Problem by Titu Andreescu).

This is totally unacceptable:

How Not to Write the Solution 1:

The above is an answer, not a solution. This ‘solution’ lacks any evidence that these solutions actually work, and doesn’t show that there are no other solutions. Moreover, it brings the reader no closer to understanding the solution.

How Not to Write the Solution 2:

The above solution is better than the first one; a motivated reader at least has a glimmer of a path to the solution, but it’s not at all clear how the original equation rearranges to the given equation, nor how the show solutions follow.

How to Write the Solution:

Often you will have to prove multiple preliminary items before tackling the main problem. In writing a proof, we often choose to separate these parts from the main proof by labeling each as a ‘Lemma’ and clearly delimiting the lemma and its proof from the rest of the solution.

Here’s a sample problem with two different solutions that employ lemmas. We’ve used a little overkill in writing the solutions with lemmas to highlight how well we can clarify solutions with lemmas. Both of these solutions are made significantly easier to read by clearly breaking the solution into pieces.

Here are two solutions.

How Not to Write the Solution 1:

(Solution method found by community member fanzha in the Olympiad Geometry class)

Sometimes the solution to a problem comes down to investigating a few different cases. In your solution, you should identify the cases clearly and show that these cases cover all possibilities.

Here’s a sample problem:

Problem: How many positive 3-digit integers are such that one digit equals the product of the other 2 digits?

(This problem comes from the Art of Problem Solving Introduction to Counting & Probability course.)

Here are two solutions:

How Not to Write the Solution:

The solution above is short, and the answer is correct, but it’s not at all clear that all possibilities have been discovered. Also, it’s pretty tough to see that we have found exactly 52 solutions – the reader is forced to go through and count themselves.

The solution below clearly covers all possible cases and leaves no doubt that the total is 52.

How to Write the Solution:

‍

Comunicacating complex idas is not ease and can b even harder wen don’t edit the presentaion of those ideas for our adience. It pays to oganize are work in ways taht are easy to read to be sur that the audiense gets the point, and to bee sure that your saying what you meen.

If I always wrote that way, nobody would ever read anything I wrote.

Proof-read and edit your work. God may do crosswords in pen, but you’re going to make mistakes. Making sure that you wrote in a way that expresses your ideas clearly and correctly is second in importance only to having the right answer.

Make sure your equations and inequalities use your variables the way you intend. You don’t want to write “abc + bcd” when you mean “abd + acd.” This not only makes deciphering the rest of your proof difficult but might also throw off your own calculations.

Practice writing proofs. We all make occasional spelling or grammar errors, but the effects of errors multiply and too many of them make otherwise good ideas unreadable. Remember that “repetition is the mother of all skill.”

Problem:

If all proofs were written this poorly I would cry:

How Not to Write the Solution:

We will manipulate the given equations to make use of the fact that the square of any real number is negative:

(𝑥+𝑦)2=(5–𝑥)2,

𝑥𝑦=3–𝑧(𝑥+𝑦)=3–𝑧(5–𝑧).

Now we note that

0≤(𝑥–𝑦)2=(𝑥+𝑦)–4𝑥𝑦.

We can substitute for both 𝑥+𝑦 and 𝑥𝑦 giving us an inequality involving only the variable 𝑧:

0≤(𝑥+𝑦)2–4𝑥𝑦=25–10𝑧+𝑧2–12+20𝑧–4𝑧2=3𝑧2+10𝑧+13.

Since this inequality holds for 𝑧 we can determine all possible values of 𝑧:

0≥−3𝑧2+10𝑧+13=−(𝑧+1)(3𝑧–13).

The iequality holds when −1≥𝑧≥13/3.

Since the given equations for 𝑥, 𝑦, and 𝑧 can be manipulated to same quadratic inequality in 𝑥, 𝑦, or 𝑧, they each have a minimum of 13/3. This happens when
𝑥=𝑦=13 and 𝑧=13/3.

Graders will be happier when reading this solution:

How to Write the Solution:

We will manipulate the given equations to make use of the fact that the square of any real number is nonnegative:

(𝑥+𝑦)2=(5–𝑥)2,

𝑥𝑦=3–𝑧(𝑥+𝑦)=3–𝑧(5–𝑧).

Now we note that

0≤(𝑥–𝑦)2=(𝑥+𝑦)2–4𝑥𝑦.

We can substitute for both 𝑥+𝑦 and 𝑥𝑦 giving us an inequality involving only the variable 𝑧:

0≤(𝑥+𝑦)2–4𝑥𝑦=25–10𝑧+𝑧2–12+20𝑧–4𝑧2=−3𝑧2+10𝑧+13.

Since this inequality holds for z we can determine all possible values of z:

0≤−3𝑧2+10𝑧+13=−(𝑧+1)(3𝑧–13).

The inequality holds when −1≤𝑧≤13/3.

Since the given equations for 𝑥, 𝑦, and 𝑧 can be manipulated to form this same quadratic inequality in𝑥, 𝑦, or 𝑧, they each have maximum possible values of 13/3. This maximum can be achieved when 𝑥=𝑦=1/3 and 𝑧=13/3.

‍

We have several shelves full of math books in our offices. When we don’t have bookends on either end, eventually the books at the ends fall over. Then more fall over, then more, and it’s a hassle to find and retrieve books without spilling others all over the place.

Similarly, when you have a complicated solution, you should place bookends on your solution so the reader doesn’t get lost in the middle. Start off saying what you’re going to do, then do it, then say what you did. Explaining your general method before doing it is particularly important with standard techniques such as contradiction or induction. For example, you might start with, ‘We will show by contradiction that there are infinitely many primes. Assume the opposite, that there are exactly 𝑛 primes ….’

When you finish your solution, make it clear you are finished. State the final result, which should be saying that you did exactly what the problem asked you to do, e.g. ‘Thus, we have shown by contradiction that there are infinitely many prime numbers.’ You can also decorate the end of proofs with such items as 𝑄𝐸𝐷 or 𝐴𝑌𝐷 or 𝑊𝑊𝑊𝑊𝑊 or Undefined control sequence \blacksquare or //.

Here’s a sample problem:

Problem: Let 𝐼 be the incenter of triangle 𝐴𝐵𝐶. Prove

(𝐼𝐴)(𝐼𝐵)(𝐼𝐶)=4𝑟2

where 𝑅 is the circumradius of 𝐴𝐵𝐶 and 𝑟 is the inradius of 𝐴𝐵𝐶.

(Problem from Sam Vandervelde of the Mandelbrot Competition. Note that the incenter of a triangle is the center of the circle inscribed in the triangle. The inradius is the radius of this circle. The circumradius is the radius of the circle that passes through the vertices of 𝐴𝐵𝐶.)

As this is our last problem, we’ll include many of our no-nos in the ‘How Not’ solution. Good luck piecing it together.

How Not to Write the Solution:

From △𝐴𝐼𝐶 we have ∠𝐴𝐼𝐶= 180∘–∠𝐴𝐶𝐼–∠𝐶𝐴𝐼= 180∘–𝛼/2–𝛾/2= 180∘–(180∘–𝛽)/2= 90∘+𝛽/2 and from △𝐸𝐵𝐶 we have ∠𝐸𝐵𝐶= ∠𝐴𝐵𝐶+∠𝐴𝐵𝑄= 𝛽+(180∘–𝛽)/2= 90∘+𝛽/2, so ∠𝐴𝐼𝐶=∠𝐸𝐵𝐶. Thus, △𝐴𝐼𝐶∼△𝐸𝐵𝐶 by Angle-Angle Similarity. By symmetry, we conclude △𝐵𝐼𝐶∼△𝐸𝐴𝐶.

[𝐴𝐼𝐸]=(𝐴𝐼)(𝐴𝐸)/2= (𝑥)(𝑏𝑦/𝑧)/2=𝑏𝑥𝑦/2𝑧, [𝐴𝐼𝐶]=𝑏𝑟/2, and [𝐸𝐵𝐶]=[𝐴𝐼𝐶](𝐵𝐶/𝐼𝐶)2= (𝑏𝑟/2)(𝑎/𝑧)2= 𝑎2𝑏𝑟/2𝑧2, so [𝐸𝐴𝐶𝐵]= 𝑏𝑥𝑦/2𝑧+𝑏𝑟/2+ 𝑎2𝑏𝑟/2𝑧2= 𝑎𝑥𝑦/2𝑧+𝑎𝑟/2+ 𝑎𝑏2𝑟/2𝑧2. Thus, (𝑏–𝑎)(𝑥𝑦/2𝑧+𝑟+𝑎𝑏𝑟/2𝑧2)=0. If 𝑏=𝑎, then 𝑎𝑏–𝑧2=𝑥𝑦𝑧/𝑟 follows from the Pythagorean Theorem and the Angle Bisector Theorem. Otherwise, 𝑎𝑏–𝑧2=𝑥𝑦𝑧/𝑟 follows immediately.

Draw altitude 𝐼𝐸 of 𝐴𝐼𝐶. [𝐸𝐼𝐶]= (𝑧2/2)sin𝛾= 𝑟(𝑠–𝑐)/2, and [𝐴𝐵𝐶]= (𝑎𝑏/2)sin𝛾= 𝑟𝑠, so [(𝑎𝑏–𝑧2)/2]sin𝛾=𝑟𝑐. Then the Law of Sines and the earlier equation give our result.

Short, ugly, and completely incomprehensible.

How to Write the Solution:

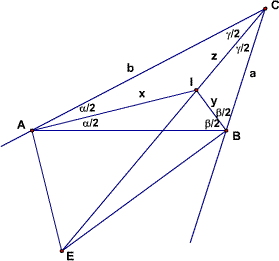
We let

𝑎=𝐵𝐶,𝑏=𝐴𝐶,𝑐=𝐴𝐵

𝑠=(𝑎+𝑏+𝑐)/2

𝛼=∠𝐵𝐴𝐶,𝛽=∠𝐴𝐵𝐶,𝛾=∠𝐴𝐵𝐶,

[𝐴𝐵𝐶]=area of polygon 𝐴𝐵𝐶

𝑥=𝐼𝐴,𝑦=𝐼𝐵,𝑧=𝐼𝐶

Let the external bisectors of angles 𝐴 and 𝐵 of △𝐴𝐵𝐶 meet at 𝐸 as shown. Point 𝐸 is equidistant from lines 𝐴𝐵, 𝐴𝐶, and 𝐵𝐶, so it is on angle bisector 𝐶𝐼 as well. We will show

[𝐸𝐴𝐶𝐵]=𝑏𝑥𝑦/2𝑧+𝑏𝑟/2+𝑎2𝑏𝑟/2𝑧2=𝑎𝑥𝑦/2𝑧+𝑎𝑟/2+𝑎𝑏2𝑟/2𝑧2²,(1)

and

(sin𝛾)(𝑎𝑏–𝑧2)/2=𝑟𝑐.(2)

From (1) we will show that 𝑎𝑏–𝑧2= 𝑥𝑦𝑧/𝑟, which we will combine with (2) and known triangle relationships to show the desired result.

Lemma 1: △𝐴𝐼𝐶∼△𝐸𝐵𝐶 and △𝐵𝐼𝐶∼△𝐸𝐴𝐶.
Proof: By symmetry, the two results are equivalent. We will show the first. Since 𝐶𝐼 bisects ∠𝐴𝐶𝐵, we have ∠𝐴𝐶𝐼=∠𝐵𝐶𝐸.

From △𝐴𝐼𝐶 we have

∠𝐴𝐼𝐶=180∘–∠𝐴𝐶𝐼–∠𝐶𝐴𝐼=180∘–𝛼/2–𝛾/2=180∘–(180∘–𝛽)/2=90∘+𝛽/2

and from △𝐸𝐵𝐶 we have

∠𝐸𝐵𝐶=∠𝐴𝐵𝐶+∠𝐴𝐵𝑄=𝛽+(180∘–𝛽)/2=90∘+𝛽/2,

so △𝐴𝐼𝐶∼△𝐸𝐵𝐶 by Angle-Angle Similarity. By symmetry, we conclude △𝐴𝐼𝐶∼△𝐸𝐵𝐶. Undefined control sequence \blacksquare

Lemma 2:

[𝐸𝐴𝐶𝐵]=𝑏𝑥𝑦/2𝑧+𝑏𝑟/2+𝑎2𝑏𝑟/2𝑧2=𝑎𝑥𝑦/2𝑧+𝑎𝑟/2+𝑎𝑏2𝑟/2𝑧2

Proof: We find the area of 𝐸𝐴𝐶𝐵 by splitting it into pieces:

[𝐸𝐴𝐶𝐵]=[𝐴𝐼𝐸]+[𝐴𝐼𝐶]+[𝐸𝐵𝐶]

First we tackle [𝐴𝐼𝐸] by showing it is a right triangle with legs 𝑥 and 𝑏𝑦/𝑧. From Lemma 1, we have △𝐵𝐼𝐶∼△𝐸𝐴𝐶. Hence, 𝐴𝐸/𝐼𝐵=𝐴𝐶/𝐼𝐶, or

𝐴𝐸=(𝐴𝐶)(𝐼𝐵)/𝐼𝐶=𝑏𝑦/𝑧.

Since

[𝐴𝐼𝐸]=(𝐴𝐼)(𝐴𝐸)/2=(𝑥)(𝑏𝑦/𝑧)/2=𝑏𝑥𝑦/2𝑧.(3)

For triangle 𝐴𝐼𝐶 we note that the altitude from 𝐼 to 𝐴𝐶 is the inradius of 𝐴𝐵𝐶, so

[𝐴𝐼𝐶]=𝑏𝑟/2.(4)

Finally, since △𝐴𝐼𝐶∼△𝐸𝐵𝐶, we have

[𝐸𝐵𝐶]=[𝐴𝐼𝐶](𝐵𝐶/𝐼𝐶)2=(𝑏𝑟/2)(𝑎/𝑧)2=𝑎2𝑏𝑟/2𝑧2.(5)

Adding (3), (4), and (5) yields

[𝐸𝐴𝐶𝐵]=𝑏𝑥𝑦/2𝑧+𝑏𝑟/2+𝑎2𝑏𝑟/2𝑧2(6)

By symmetry, we note that [𝐸𝐴𝐶𝐵] also equals our expression in (6) with 𝑎 and 𝑏 interchanged and 𝑥 and 𝑦 interchanged. Hence, we have the desired

[𝐸𝐴𝐶𝐵]=𝑏𝑥𝑦/2𝑧+𝑏𝑟/2+𝑎2𝑏𝑟/2𝑧2=𝑎𝑥𝑦/2𝑧+𝑎𝑟/2+𝑎𝑏2𝑟/2𝑧2

Undefined control sequence \blacksquare

Lemma 3 : 𝑎𝑏–𝑧2=𝑥𝑦𝑧/𝑟.
Proof: Rearranging our result from Lemma 1 yields

(𝑏𝑥𝑦/2𝑧+𝑏𝑟/2+𝑎2𝑏𝑟/2𝑧2)–(𝑎𝑥𝑦/2𝑧+𝑎𝑟/2+𝑎𝑏2𝑟/2𝑧2)=0

(𝑏𝑥𝑦/2𝑧–𝑎𝑥𝑦/2𝑧)+(𝑏𝑟/2–𝑎𝑟/2)+(𝑎2𝑏𝑟/2𝑧2–𝑎𝑏2𝑟/2𝑧2)=0

(𝑏−𝑎)(𝑥𝑦/2𝑧)+(𝑏–𝑎)(𝑟/2)–(𝑏–𝑎)(𝑎𝑏𝑟/2𝑧2)=0

(𝑏–𝑎)(𝑥𝑦/2𝑧+𝑟/2–𝑎𝑏𝑟/2𝑧2)=0

Thus, one of the terms in this product equals 0.

Case 1: 𝑏–𝑎=0.

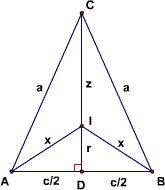
If 𝑏=𝑎 then 𝐴𝐵𝐶 is isosceles and 𝛼=𝛽. Hence, the extension of angle bisector 𝐶𝐼 is perpendicular to 𝐴𝐵 at point 𝐷 as shown. Since 𝐼 is the incenter of 𝐴𝐵𝐶 and 𝐼𝐷⊥𝐴𝐵, 𝐼𝐷=𝑟 since 𝐼𝐷 is an inradius of 𝐴𝐵𝐶. Also,

∠𝐼𝐴𝐵=𝛼/2=𝛽/2=∠𝐼𝐵𝐴,

so 𝐼𝐵=𝐼𝐴 (i.e. 𝑥=𝑦). Thus, the equation we wish to prove, 𝑎𝑏–𝑧2= 𝑥𝑦𝑧/𝑟, is in this case equivalent to

𝑎2–𝑧2=𝑥2𝑧/𝑟.(7)

From right triangles 𝐶𝐴𝐷 and 𝐼𝐴𝐷, we have

(𝑐/2)2+𝑟2=𝑥2,(8)

(𝑐/2)2+(𝑧+𝑟)2=𝑎2.(9)

The Angle Bisector Theorem gives us 𝑎/𝑧= 𝐴𝐶/𝐶𝐼= 𝐴𝐷/𝐷𝐼= (𝑐/2)/𝑟, or

𝑐/2=𝑎𝑟/𝑧.(10)

Substituting (10) into (8) yields

𝑎2𝑟2/𝑧2+𝑟2=𝑥2,

𝑎2𝑟2+𝑟2𝑧2=𝑥2𝑧2,

(𝑟/𝑧)(𝑎2+𝑧2)=𝑥2𝑧/𝑟.(11)

Substituting (10) into (9) gives

𝑎2𝑟2/𝑧2+(𝑧+𝑟)2=𝑎2,

𝑎2𝑟2+𝑧2(𝑧+𝑟)2=𝑎2𝑧2,

𝑧2(𝑧+𝑟)2=𝑎2𝑧2–𝑎2𝑟2,

𝑧2(𝑧+𝑟)2=𝑎2(𝑧2–𝑟2),

𝑧(𝑧+𝑟)=𝑎2(𝑧–𝑟),

𝑎2𝑟+𝑧2𝑟=𝑎2𝑧–𝑧3,

(𝑟/𝑧)(𝑎2+𝑧2)=𝑎2–𝑧2.(12)

Combining (11) and (12) gives us the desired 𝑎2–𝑧2=𝑥2𝑧/𝑟.

Case 2: 𝑥𝑦/2𝑧+𝑟/2–𝑎𝑏𝑟/2𝑧2=0.

Multiplying this equation by 2𝑧2/𝑟 yields

𝑥𝑦𝑧/𝑟+𝑧2–𝑎𝑏=0,

from which the desired 𝑎𝑏–𝑧2=𝑥𝑦𝑧/𝑟 immediately follows.

Thus, the lemma is proved. Undefined control sequence \blacksquare

Lemma 4: (sin𝛾)(𝑎𝑏–𝑧2)/2=𝑟𝑐.

Proof:

We draw altitude 𝐼𝐹 perpendicular to 𝐵𝐶 as shown. We employ the following known triangle relationships:

𝐶𝐹[𝐴𝐵𝐶]=𝑠–𝑐=(𝑎𝑏/2)sin𝛾=𝑟𝑠

Just as [𝐴𝐵𝐶]=(𝑎𝑏/2)sin𝛾, we have

𝐶𝐹𝐶𝐹𝐶𝐹𝐶𝐹=[(𝐶𝐹)(𝐼𝐶)/2]sin(𝛾/2)=[𝑧cos(𝛾/2)][𝑧/2sin(𝛾/2)]=(𝑧2/2)cos(𝛾/2)sin(𝛾/2)=(𝑧2/4)sin𝛾

where we have used sin2𝛾= 2sin𝛾cos𝛾 in the last step.

Since 𝐶𝐹𝐼 is right, we have [𝐶𝐹𝐼]=𝑟(𝑠–𝑐)/2. Hence, we have two expressions for [𝐴𝐵𝐶]–2[𝐶𝐹𝐼]:

(𝑎𝑏/2)sin𝛾–2(𝑧2/4)sin𝛾[(𝑎𝑏–𝑧2/2]sin𝛾=𝑟𝑠–2[𝑟(𝑠–𝑐/2]=𝑟𝑠

as desired. Undefined control sequence \blacksquare

We now complete our proof. Dividing the result of Lemma 4 by (sin𝛾)/2 gives

𝑎𝑏–𝑧2=2𝑟𝑐/(sin𝛾).

Since Lemma 3 gives us 𝑎𝑏–𝑧2=𝑥𝑦𝑧/𝑟 and the Extended Law of Sines gives us sin𝛾=𝑐/2𝑅, the equation above becomes

𝑥𝑦𝑧/𝑟𝑥𝑦𝑧/𝑟𝑥𝑦𝑧=2𝑟𝑐/(𝑐/2𝑅)=4𝑅𝑟=4𝑅𝑟2

Thus, we have shown that if 𝐼 is the incenter of triangle 𝐴𝐵𝐶, we have

(𝐼𝐴)(𝐼𝐵)(𝐼𝐶)=4𝑅𝑟2,

where 𝑅 is the circumradius of 𝐴𝐵𝐶 and 𝑟 is the inradius of 𝐴𝐵𝐶.

‍

Note, we proved some intermediate results we probably didn’t have to (such as the fact that 𝐸 is on ray 𝐶𝐼) when the results were quick and easy to prove. Others we stated by fiat, such as [𝐴𝐵𝐶]=𝑟𝑠, since the proofs are more involved, and we feel pretty safe that these results can be cited as known results without proof.

The above is a pretty daunting proof. What our solution doesn’t give is any indication of how we might have come up with this solution. If you didn’t find the above solution on your own, see if you can figure out how you might have come up with it now that you have seen it.

‍